
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


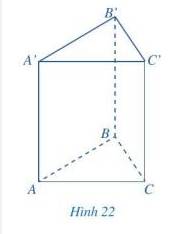
Hình lăng trụ đứng tam giác có:
+) 5 mặt gồm: ABC; A’B’C’; ABB’A’; BCC’B’; ACC’A’
+) 9 cạnh gồm: AB; BC;CA;A’B’;B’C’;C’A’; AA’; BB’; CC’
+) 6 đỉnh gồm: A;B;C; A’;B’;C’.

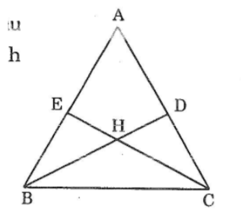
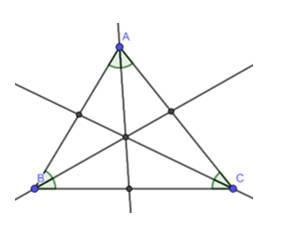
Các tam giác = nhau là :
\(\Delta ABD\) và \(\Delta BDC\)
\(\Delta BEH\) và \(\Delta CDH\)
\(\Delta AEC\) và \(\Delta BEC\)
Tick minh ha

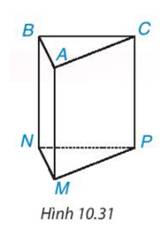
+ 2 mặt đáy : ABC, MNP
+ 3 mặt bên : ACPM, BAMN, BCPN
+ Cạnh đáy : NM, MP, NP, AB, BC, CA
+ Cạnh bên : AM, BN, CP

a)\(\left( {\frac{{ - 5}}{8}} \right) + \left( {\frac{3}{{ - 8}}} \right) = \left( {\frac{{ - 5}}{8}} \right) + \left( {\frac{{ - 3}}{8}} \right) = - 1\)
Vậy dấu cần điền là “=”.
b)\(\left( {\frac{{ - 13}}{{22}}} \right) + \left( {\frac{{ - 5}}{{22}}} \right) = \frac{{ - 18}}{{22}} = \frac{{ - 9}}{{11}} < \frac{{ - 8}}{{11}}\).
Vậy dấu cần điền là “>”.
c) \(\frac{1}{6} + \left( {\frac{{ - 3}}{4}} \right) = \frac{2}{{12}} + \left( {\frac{{ - 9}}{{12}}} \right) = \frac{{ - 7}}{{12}}\)
\(\frac{1}{{14}} + \left( {\frac{{ - 4}}{7}} \right) = \frac{1}{{14}} + \left( {\frac{{ - 8}}{{14}}} \right) = \frac{{ - 7}}{{14}}\)
Mà 12 < 14 nên \(\frac{{ 7}}{{12}} > \frac{{ 7}}{{14}}\), do đó \(\frac{{ - 7}}{{12}} < \frac{{ - 7}}{{14}}\)
Vậy dấu cần điền là “<”.

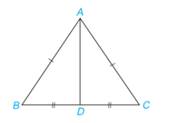
a) Xét hai tam giác ABD và ACD có:
AB=AC
AD chung
BD=DC
=>\(\Delta \)ABD = \(\Delta \)ACD (c.c.c)
b) Do \(\Delta \)ABD = \(\Delta \)ACD nên \(\widehat B = \widehat C\)( 2 góc tương ứng)
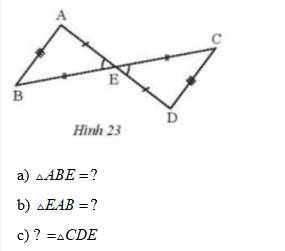


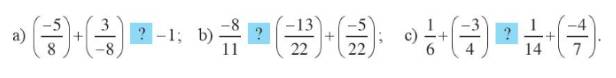
a) Tam giác ABE = tam giác DCE
b) Tam giác EAB = tam giác ECD
C) Tam giác ABE = tam giác CDE
\(a,\Delta ABE=\Delta DCE\\ b,\Delta EAB=\Delta ECD\\ c,\Delta BAE=\Delta CDE\)