Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Qua đỉnh C của hình bình hành ABCD kẻ đường thẳng song song với BD cắt AB ở E, cắt AD ở F
a.Tứ giác BECD là hình gì Vì sao
b.Chứng minh 3 đừng thẳng AC, BF, DE đồng quy
Qua đỉnh C của hình bình hành ABCD kẻ đường thẳng song song với BD cắt AB ở E, cắt AD ở F
a.Tứ giác BECD là hình gì Vì sao
b.Chứng minh 3 đừng thẳng AC, BF, DE đồng quy


Áp dụng định lý Thalès, ta có:
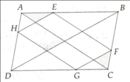
HE // BD \(\Rightarrow\frac{AH}{AD}=\frac{AE}{AB}\)(1)
EF // AC \(\Rightarrow\frac{AE}{AB}=\frac{FC}{BC}\)(2)
FG // BD \(\Rightarrow\frac{FC}{BC}=\frac{GC}{DC}\)(3)
Từ (1),(2),(3) suy ra \(\frac{AH}{AD}=\frac{GC}{DC}\Rightarrow AH.CD=AD.CG\left(đpcm\right)\)

A B C D E F
a/
Ta có
AB//CD (cạnh đối hbh) => BE//CD
CE//BD (gt)
=> BECD là hình bh (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
b/
Ta có
BE=CD (cạnh đối hbh)
AB=CD (cạnh đối hbh)
=> BE=AB => BF là đường trung tuyến của tg AEF
Ta có
CF//BD (gt)
AD//BC (cạnh đối hbh) => DF//BC
=> BCFD là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
Ta có
BC=AD (cạnh đối hbh)
BC=DF (cạnh đối hbh)
=> AD=DF => DE là đường trung tuyến của tg AEF
Ta có
BD=CE (cạnh đối hbh)
BD=CF (cạnh đối hbh)
=> CE=CF => AC là trung tuyến của tg AEF
=> AC; BF; DE đồng quy (trong tg 3 đường trung tuyến đồng quy)

A) ta có:
AD//BC (ABCD là hình bình hành)
=>góc DAB= góc CBE(2 góc so le trong)
và góc ADB=góc DBC (2 góc so le trong)
mà góc DBC= góc BCE ( BD//CE)
nên góc ADB= góc BCE
Xét tam giác ABD và tam giác BEC
góc DAB= góc CBE(chứng minh trên)
góc ADB= góc BCE(chứng minh trên)
AD=BC(ABCD là hình bình hành)
suy ra: tam giác ABD = tam giác BEC(g-c-g)
suy ra: BD=CE(2 cạnh tương ứng)
mà BD//CE(giả thiết)
nên BECD là hình bình hành
a: Xét tứ giác BECD có
BE//CD
BD//CE
Do đó: BECD là hình bình hành