Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

T P F ht
T=\(\dfrac{P}{cos\alpha}\)=\(\dfrac{\sqrt{2}}{4}N\)
tan\(\alpha=\dfrac{F_{ht}}{P}\)=\(\dfrac{\omega^2.sin\alpha.l.m}{m.g}\)\(\Rightarrow\)\(\omega\approx5,318\) (rad/s)
T=\(\dfrac{2\pi}{\omega}\)\(\approx\)1,18s

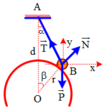
Khi ôtô chuyển động qua cầu, ôtô chịu tác dụng của hai lực. Trọng lực \(\overrightarrow{P}\)và phản lực \(\overrightarrow{N}\) do mặt cầu tác dụng lên ôtô như hình vẽ. Hợp lực của hai lực này đóng vai trò là lực hướng tâm, \(\overrightarrow{P}+\overrightarrow{N}\)= \(\overrightarrow{ma_{ht}}\)
Vậy áp lực do ô tô tác dụng xuống mặt cầu bằng 13 000N
So sánh: Áp lực F = N = 13000 < P = mg = 15000 N
Nhận xét: Khi ôtô chuyển động trên mặt cong (vồng lên) áp lực của ôtô xuống mặt cầu nhỏ hơn so với trọng lực của nó.

Chọn gốc thế năng tại \(A\left(Z_A=0\right)\)
Ta có:\(W_A=W_B\)
\(\Leftrightarrow\frac{1}{2}mv_A^2=\frac{1}{2}mv_B^2+mgZ_B\)
\(\Leftrightarrow v_A^2=v_B^2+2gZ_B\)
\(\Rightarrow v_A^2=33,31\)
Áp dụng định luật II niuton tại điểm A chiếu lên phương dây treo ta có
\(T=P+m\frac{v_A^2}{l}\)
Thay số vào được T = 7,643 N
\(->chọn.D\)

a) Chọn gốc thế năng trọng trường tại C ( Hình 92).
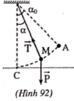
Theo định luật bảo toàn cơ năng: W A = W M
![]()
Vận tốc của m tại một điểm trên quỹ đạo ( ứng với góc lệch α )
![]()
Vận tốc v sẽ đạt cực đại khi cos α = 1 hay α = 0 .
![]()
b) Phương trình chuyển động của m: P → + T → = m a →
Chiếu phương trình lên phương bán kính đi qua M, chiều dương hướng vào điểm treo:
![]()
Thay ![]() vào phương trình của T ta được:
vào phương trình của T ta được:
Lực căng dây tại M ( ứng với góc lệch: T = m g 3 cos α - 2 cos α 0
Lực căng T đạt cực đại khi cos α = 1 hay α = 0 : T = m g 3 - 2 cos α 0

Gọi vận tốc sau va chạm lần lượt là \(v_1\) và \(v_2\).
Bảo toàn động lượng:
\(m_2v=m_1v_1+m_2v_2\)
\(\Rightarrow v_1+0,02v_2=1\left(1\right)\)
Bảo toàn năng lượng:
\(\frac{m_2v^2}{2}=\frac{m_1v^2_1}{2}+\frac{m_2v^2_2}{2}\)
hay:
\(m_2v^2=m_1v^2_1+m_2v^2_2\)
\(\Rightarrow v^2_1+0,02v^2_2=50\left(2\right)\)
Giải (1) và (2):
\(v_1=2,96\left(m\text{/}s\right)\)
\(v_2=-48\left(m\text{/}s\right)\)
Góc lệch cực đại \(\alpha\) dễ dàng đc tính theo công thức:
\(m_1gl\left(1-\cos\alpha\right)=\frac{m_1v^2_1}{2}\)
\(\alpha=65^0\)
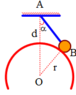
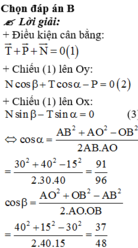
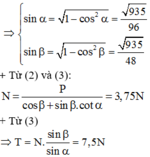
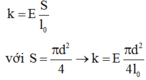
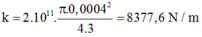
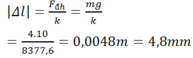
+ Vì quả cầu chuyển động đu đưa theo cung tròn nên, ta có: F - P = m α h t
↔ k . x - m g = m v 2 R ↔ E . S l 0 x - m g = m v 2 l 0 + x + D 2 ↔ E πd 2 4 l 0 x - m g ≈ m v 2 l 0 + D 2 → x = 4 l 0 m E πd 2 v 2 l 0 + D 2 + g = 4 . 2 , 8 . 4 1 , 86 . 10 11 . π . 0 , 9 . 10 - 3 2 5 2 2 , 8 + 0 , 1 2 + 10 ≈ 1 , 8 . 10 - 3 m
Khoảng trống tối thiểu từ quả cầu đến sàn là: l m i n = 3 - 2 , 8 + 0 , 1 + 0 , 0018 = 0 , 0982 m = 9 , 82 c m
Đáp án: A