Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Lực tương tác giữa hai điện tích là:
F = \(\frac{k.\left|q_1.q_2\right|}{r^2}\) = \(\frac{9.10^9.\left|-10^{-8}.4.10^{-8}\right|}{0,06^2}\) = 10-3 (N)
b)

Gọi \(\overrightarrow{F_{13}}\) là lực do điện tích q1 tác dụng lên q3
\(\overrightarrow{F_{23}}\) là lực do điện tích q2 tác dụng lên q3
\(\overrightarrow{F'}\) là tổng hợp lực của \(\overrightarrow{F_{13}}\) và \(\overrightarrow{F_{23}}\)
Ta có lực điện tổng hợp tác dụng lên q3 là: \(\overrightarrow{F'}\) = \(\overrightarrow{F_{13}}\) + \(\overrightarrow{F_{23}}\)
mà \(\overrightarrow{F_{13}}\) \(\uparrow\uparrow\) \(\overrightarrow{F_{23}}\) nên về độ lớn: F' = F13 + F23 = \(\frac{k.\left|q_1.q_3\right|}{r_{13}^2}\) + \(\frac{k.\left|q_2.q_3\right|}{r_{23}^2}\)
= \(\frac{9.10^9.\left|-10^{-8}.2.10^{-8}\right|}{0,03^2}\) + \(\frac{9.10^9.\left|4.10^{-8}.2.10^{-8}\right|}{0,03^2}\) = 0,01 (N)
c) Theo đề bài ta có: \(\overrightarrow{F'}\) = \(\overrightarrow{F_{13}}\) + \(\overrightarrow{F_{23}}\) = \(\overrightarrow{0}\) ⇒ \(\overrightarrow{F_{13}}\) = \(-\)\(\overrightarrow{F_{23}}\)
\(\overrightarrow{F_{13}}\), \(\overrightarrow{F_{23}}\) cùng giá C ∈ AB, ngược chiều \(\overrightarrow{F_{13}}\) \(\downarrow\uparrow\) \(\overrightarrow{F_{23}}\)(C nằm ngoài AB, gần A hơn) và độ lớn: F13 = F23
⇔ \(\frac{k.\left|q_1.q_3\right|}{r_{13}^2}\) = \(\frac{k.\left|q_2.q_3\right|}{r_{23}^2}\)
⇔ \(\frac{r_{13}}{r_{23}}\) = \(\sqrt{\left|\frac{q_1}{q_2}\right|}\) = \(\frac{1}{2}\) ⇔ 2.r13 - r23 = 0 (1)
mà r23 - r13 = 0,06 (2)
Từ (1) và (2) ⇒ \(\left\{{}\begin{matrix}r_{13}=0,06\left(m\right)\\r_{23}=0,12\left(m\right)\end{matrix}\right.\)
Vậy ...

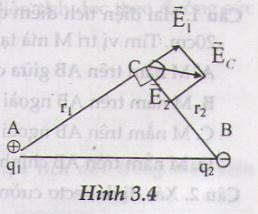
13. Hai điện tích điểm A và B cách nhau 5cm trong chân không có hai điện tích q1 = +16.10-8 C và q2 = - 9.10-8 C. Tính cường độ điện trường tổng hợp và vẽ vectơ cường độ điện trường tại điểm C nằm cách A một khoảng 4cm và cách B một khoảng 3cm.
Hướng dẫn giải.
Đặt AC = r1 và BC = r2 . Gọi −→E1E1→ và −→E2E2→ lần lượt là cường độ điện trường do q1 và q2 gây ra ở C (Hình 3.4).
E1=k.q1εr21E1=k.q1εr12= 9.105 V/m (Hướng theo phương AC).
E1=k.q2εr22E1=k.q2εr22 = 9.105 V/m (Hướng theo phương CB).
Vì tam giác ABC là tam giác vuông nên hai vectơ −→E1E1→ và −→E2E2→ vuông góc với nhau.
Gọi −→ECEC→ là vectơ cường độ điện trường tổng hợp :
−→ECEC→ = −→E1E1→ + −→E2E2→ => EC=√2E1=12,7.105EC=2E1=12,7.105 V/m.
Vectơ −→ECEC→ làm với các phương AC và BC những góc 450 và có chiều như hình vẽ.

+ - A B C q1 q2 E1 E2 E
Nhận xét: Do \(AB^2=AC^2+BC^2\) nên tam giác ABC vuông tại C.
Điện trường tổng hợp tại C là: \(\vec{E}=\vec{E_1}+\vec{E_2}\)
Suy ra độ lớn: \(E=\sqrt{E_1^2+E_2^2}\) (*) (do \(\vec{E_1}\) vuông góc với \(\vec{E_2}\) )
\(E_1=9.10^9.\dfrac{16.10^{-8}}{0,04^2}=9.10^5(V/m)\)
\(E_1=9.10^9.\dfrac{9.10^{-8}}{0,03^2}=9.10^5(V/m)\)
Thay vào (*) ta được \(E=9\sqrt2.10^5(V/m)\)

Hai điện tích đẩy nhau => q1 và q2 cùng dấu
q1 + q2 = – 6.10-6 C (1) => |q1q2| = q1q2
F = 1,8 N; |q1| > |q2|; r = 20cm = 20.10-2m; ε = 1
\(F=9.10^9.\frac{\left|q_1q_2\right|}{r^2}\Rightarrow\left|q_1q_2\right|=8.10^{-12}\) (2)
Từ (1) và (2) => q1 = – 4.10-6 C; q2 = – 2.10-6 C.
đề ngữ văn lớp mấy vậy sao để là vật lý 11
lớp 9 chị ạ