NT
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
CM
17 tháng 2 2018
TXĐ: R \ {-1}
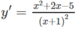
y' = 0 ⇔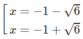 
Vậy hàm số đã cho đồng biến trên các khoảng (− ∞ ; −1 − 6 ), (−1 + 6 ; + ∞ ) và nghịch biến trên các khoảng (−1 − 6 ; −1),(−1; −1 + 6 )
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 6 2021
1.
\(f'\left(x\right)=\left(x^2-1\right)\left(x-2\right)^2\left(x-3\right)\) có các nghiệm bội lẻ \(x=\left\{-1;1;3\right\}\)
Sử dụng đan dấu ta được hàm đồng biến trên các khoảng: \(\left(-1;1\right);\left(3;+\infty\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-1\right);\left(1;3\right)\)
2.
\(y'=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=0\\x=1\end{matrix}\right.\)
Lập bảng xét dấu y' ta được hàm đồng biến trên \(\left(-1;0\right);\left(1;+\infty\right)\)
Hàm nghịch biến trên \(\left(-\infty;-1\right);\left(0;1\right)\)
AH
Akai Haruma
Giáo viên
10 tháng 8 2018
Lời giải:
Ta có:
\(y'=-3x^2+6x\)
\(y'>0\Leftrightarrow -3x^2+6x>0\Leftrightarrow 0< x< 2\) (khoảng đồng biến)
\(y'< 0\Leftrightarrow -3x^2+6x< 0\Leftrightarrow x<0\) hoặc \(x>2\), tức là \(x\in (-\infty, 0)\) hoặc \(x\in (2;+\infty)\) (khoảng nghịch biến)
Từ đây ta suy ra A là đáp án đúng.
LP
0
N
2
AH
Akai Haruma
Giáo viên
16 tháng 5 2021
1. TXĐ: $x\in [1;2]$
Ta có:
$y'=\frac{3-2x}{2\sqrt{-x^2+3x-2}}=0\Leftrightarrow x=\frac{3}{2}$
Vậy hàm số có điểm tới hạn $x=\frac{3}{2}$
Vẽ BBT với các mốc $x=1; x=\frac{3}{2}; x=2$ ta thấy hàm số đồng biến trên $(1;\frac{3}{2})$ và nghịch biến trên $(\frac{3}{2};2)$
AH
Akai Haruma
Giáo viên
16 tháng 5 2021
2.
TXĐ: $x\in\mathbb{R}$
$y=\sqrt{x^2+x+1}\Rightarrow y'=\frac{2x+1}{2\sqrt{x^2+x+1}}=0$
$\Leftrightarrow x=\frac{-1}{2}$
Vẽ BBT với các mốc $-\infty; \frac{-1}{2};+\infty$ ta thấy hàm số đồng biến trên $(\frac{-1}{2};+\infty)$ và nghịch biến trên $(-\infty; \frac{-1}{2})$
PT
1
CM
24 tháng 3 2018
TXĐ: R \ {2}
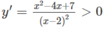
(do x 2 − 4x + 7 x 2 − 4x + 7 có ∆ ' = - 3 < 0)
Vậy hàm số đã cho đồng biến trên các khoảng (− ∞ ;2),(2;+ ∞ )