Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \({\cos ^2}\alpha + {\sin ^2}\alpha = 1\)
b) \(\tan \alpha .\cot \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}.\frac{{\cos \alpha }}{{\sin \alpha }} = 1\)
c) \(\frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} + \frac{{{{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} = {\tan ^2}\alpha + 1\)
d) \(\frac{1}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha }}{{{{\sin }^2}\alpha }} + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = 1 + {\cot ^2}\alpha \)

a, Ta có: \(sin^2\alpha+cos^2\alpha=1\Leftrightarrow\left(\dfrac{3}{5}\right)^2+cos^2\alpha=1\Leftrightarrow cos\alpha=\pm\dfrac{4}{5}\)
Vậy đẳng thức có thể đồng thời xảy ra.
b, Ta có: \(1+cot^2\alpha=\dfrac{1}{sin^2\alpha}\Rightarrow1+cot^2\alpha=\dfrac{1}{\left(\dfrac{1}{3}\right)^2}\Rightarrow cot\alpha=\pm2\sqrt{2}\)
Hai đẳng thức không thể đồng thời xảy ra.
c, Ta có: \(tan\alpha\cdot cot\alpha=1\Rightarrow3\cdot cot\alpha=1\Rightarrow cot\alpha=\dfrac{1}{3}\)
Đẳng thức có thể đồng thời xảy ra.

a) Ta có:
\(\begin{array}{l}{\sin ^4}\alpha - {\cos ^4}\alpha = 1 - 2{\cos ^2}\alpha \\ \Leftrightarrow \left( {{{\sin }^2}\alpha + {{\cos }^2}\alpha } \right)\left( {{{\sin }^2}\alpha - {{\cos }^2}\alpha } \right) = 1 - 2{\cos ^2}\alpha \\ \Leftrightarrow {\sin ^2}\alpha - {\cos ^2}\alpha - 1 + 2{\cos ^2}\alpha = 0\\ \Leftrightarrow {\sin ^2}\alpha + {\cos ^2}\alpha - 1 = 0\\ \Leftrightarrow 1 - 1 = 0\\ \Leftrightarrow 0 = 0\end{array}\)
Đẳng thức luôn đúng
b) Ta có:
\(\begin{array}{l}\tan \alpha + \cot \alpha = \frac{1}{{\sin \alpha .\cos \alpha }}\\ \Leftrightarrow \frac{{\sin \alpha }}{{\cos \alpha }} + \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{1}{{\sin \alpha .\cos \alpha }}\\ \Leftrightarrow \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{\cos \alpha .\sin \alpha }} = \frac{1}{{\sin \alpha .\cos \alpha }}\\ \Leftrightarrow \frac{1}{{\sin \alpha .\cos \alpha }} = \frac{1}{{\sin \alpha .\cos \alpha }}\end{array}\)
Đẳng thức luôn đúng


a) Trong Hình 5, M là điểm biểu diễn của góc lượng giác \(\alpha \) trên đường tròn lượng giác. Ta có:
OK = MH = \(\sin \alpha \)
OH = KM = \(\cos \alpha \)
\(\begin{array}{l}O{M^2} = O{H^2} + M{H^2}\\ \Rightarrow 1 = {\sin ^2}\alpha + {\cos ^2}\alpha \end{array}\)
b) \(1 + {\tan ^2}\alpha = \frac{{{{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{1}{{{{\cos }^2}\alpha }}\)

1) \(cot\alpha=\sqrt[]{5}\Rightarrow tan\alpha=\dfrac{1}{\sqrt[]{5}}\)
\(C=sin^2\alpha-sin\alpha.cos\alpha+cos^2\alpha\)
\(\Leftrightarrow C=\dfrac{1}{cos^2\alpha}\left(tan^2\alpha-tan\alpha+1\right)\)
\(\Leftrightarrow C=\left(1+tan^2\alpha\right)\left(tan^2\alpha-tan\alpha+1\right)\)
\(\Leftrightarrow C=\left(1+\dfrac{1}{5}\right)\left(\dfrac{1}{5}-\dfrac{1}{\sqrt[]{5}}+1\right)\)
\(\Leftrightarrow C=\dfrac{6}{5}\left(\dfrac{6}{5}-\dfrac{\sqrt[]{5}}{5}\right)=\dfrac{6}{25}\left(6-\sqrt[]{5}\right)\)
1: \(cota=\sqrt{5}\)
=>\(cosa=\sqrt{5}\cdot sina\)
\(1+cot^2a=\dfrac{1}{sin^2a}\)
=>\(\dfrac{1}{sin^2a}=1+5=6\)
=>\(sin^2a=\dfrac{1}{6}\)
\(C=sin^2a-sina\cdot\sqrt{5}\cdot sina+\left(\sqrt{5}\cdot sina\right)^2\)
\(=sin^2a\left(1-\sqrt{5}+5\right)=\dfrac{1}{6}\cdot\left(6-\sqrt{5}\right)\)
2: tan a=3
=>sin a=3*cosa
\(1+tan^2a=\dfrac{1}{cos^2a}\)
=>\(\dfrac{1}{cos^2a}=1+9=10\)
=>\(cos^2a=\dfrac{1}{10}\)
\(B=\dfrac{3\cdot cosa-cosa}{27\cdot cos^3a+3\cdot cos^3a+2\cdot3\cdot cosa}\)
\(=\dfrac{2\cdot cosa}{30cos^3a+6cosa}=\dfrac{2}{30cos^2a+6}\)
\(=\dfrac{2}{3+6}=\dfrac{2}{9}\)

+) Nửa đường tròn đơn vị: nửa đường tròn tâm O, bán kính R = 1 nằm phía trên trục hoành (H.3.2).
+) Với mỗi góc \(\alpha ({0^o} \le \alpha \le {180^o})\)có duy nhất điểm \(M({x_0};{y_0})\) trên nửa đường tròn đơn vị nói trên để \(\widehat {xOM} = \alpha .\) Khi đó:
\(\sin \alpha = {y_0}\) là tung độ của M
\(\cos \alpha = {x_0}\) là hoành độ của M
\(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{{y_0}}}{{{x_0}}}(\alpha \ne {90^o})\)
\(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{{{x_0}}}{{{y_0}}}(\alpha \ne {0^o},\alpha \ne {180^o})\)

Do \(\alpha\in\left(\frac{\pi}{2};\frac{3\pi}{4}\right)\Rightarrow sin\alpha>0;cos\alpha< 0;tan\alpha< 0\)
\(\frac{tana}{cota}=\frac{\sqrt{5}-1}{\sqrt{5}+1}\Leftrightarrow tan^2a=\frac{\sqrt{5}-1}{\sqrt{5}+1}=\frac{\left(\sqrt{5}-1\right)^2}{4}\Rightarrow tana=\frac{1-\sqrt{5}}{2}\Rightarrow cota=\frac{-1-\sqrt{5}}{2}\)
\(1+tan^2a=\frac{1}{cos^2a}\Rightarrow cos^2a=\frac{1}{1+tan^2a}=\frac{5+\sqrt{5}}{10}\)
\(\Rightarrow sin^2a=1-cos^2a=\frac{5-\sqrt{5}}{10}\)
\(sin2a=2sina.cosa=2tana.cos^2a=-\frac{2\sqrt{5}}{5}\)
Thay vào ta được:
\(P=...\)
Bạn tự thay số và bấm máy

\(a,\dfrac{1}{tan\alpha+1}+\dfrac{1}{cot\alpha+1}\\ =\dfrac{cot\alpha+1+tan\alpha+1}{\left(tan\alpha+1\right)\left(cot\alpha+1\right)}\\ =\dfrac{tan\alpha+cot\alpha+2}{tan\alpha\cdot cot\alpha+tan\alpha+cot\alpha+1}\\ =\dfrac{tan\alpha+cot\alpha+2}{tan\alpha+cot\alpha+2}\\ =1\)
\(b,cos\left(\dfrac{\pi}{2}-\alpha\right)-sin\left(\pi+\alpha\right)\\ =sin\alpha+sin\alpha\\ =2sin\alpha\)
\(c,sin\left(\alpha-\dfrac{\pi}{2}\right)+cos\left(-\alpha+6\pi\right)-tan\left(\alpha+\pi\right)cot\left(3\pi-\alpha\right)\\ =-sin\left(\dfrac{\pi}{2}-\alpha\right)+cos\left(\alpha\right)-tan\left(\alpha\right)cot\left(\pi-\alpha\right)\\ =-cos\left(\alpha\right)+cos\left(\alpha\right)+tan\left(\alpha\right)\cdot cot\left(\alpha\right)\\ =1\)
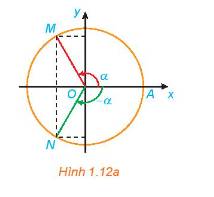
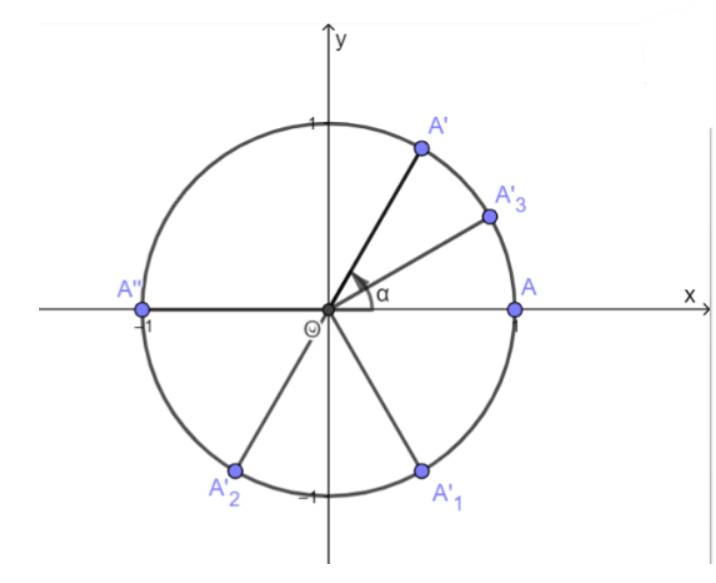
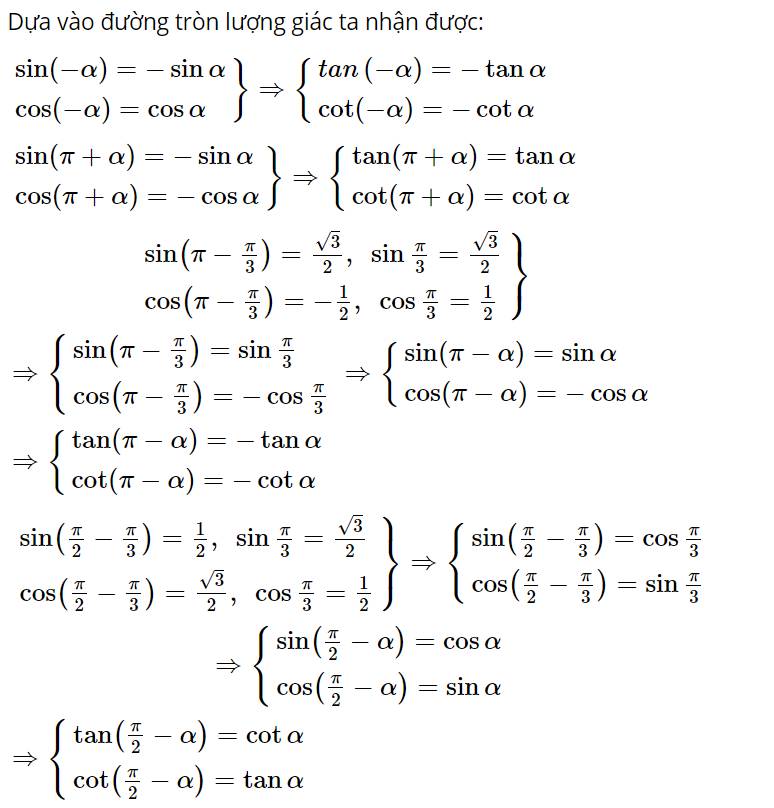
a) Hai điểm M và N đối xứng nhau qua hệ trục Oxy.
Suy ra
\(\cos ( - \alpha )\)=\(\cos \alpha \); \(\sin ( - \alpha )\)= \( - \sin \alpha \)
b) Ta có:
\(\tan ( - \alpha )\) =\( - \tan \alpha \); \(\cot ( - \alpha )\)\( - \cot \alpha \)