Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) miền xác định của \(f\) là \(D=R\backslash\left\{\pm1\right\}\)
\(\text{∀}x\in D\), ta có: \(-x\in D\) và \(f\left(-x\right)=\frac{2x^4-x^2+3}{x^2-2}=f\left(x\right)\)
\(\Rightarrow\) \(f\) là hàm số chẵn
b) Ta có: \(\left|2x+1\right|-\left|2x-1\right|\ne0\)\(\Leftrightarrow\left|2x+1\right|\ne\left|2x-1\right|\)
\(\Leftrightarrow\left(2x+1\right)^2\ne\left(2x-1\right)^2\)
\(\Leftrightarrow x\ne0\)
\(\Rightarrow\) Miền xác định của \(f\) là \(D=R\backslash\left\{0\right\}\)
khi đó \(\text{∀}x\in D\) thì \(-x\in D\) và :
\(f\left(-x\right)=\frac{\left|-2x+1\right|+\left|-2x-1\right|}{\left|-2x+1\right|-\left|-2x-1\right|}\)\(=\frac{\left|2x-1\right|+\left|2x+1\right|}{\left|2x-1\right|-\left|2x+1\right|}\)\(=-\frac{\left|2x+1\right|+\left|2x-1\right|}{\left|2x+1\right|-\left|2x-1\right|}\)
\(=-f\left(x\right)\Rightarrow f\) là hàm số lẻ

a)TXĐ D=[-2:2]
\(\forall x\in D\Rightarrow-x\in D\)
f(-x)=\(\sqrt{2-\left(-x\right)}\) +\(\sqrt{2-x}\) =\(\sqrt{2+x}+\sqrt{2-x}=f\left(x\right)\)
Hàm số đồng biến
Câu b) c) giống rồi tự xử nha
d)\(Đk:x^2-4x+4\ge0\Leftrightarrow\left(x-2\right)^2\ge0\)
TXĐ D=R
\(\forall x\in D\Rightarrow-x\in D\)
\(f\left(-x\right)=\sqrt[]{\left(-x\right)^2+4x+4}+\left|2-x\right|=\sqrt{x^2+4x+4}+\left|2-x\right|\ne\mp f\left(x\right)\)
Hàm số không chẵn không lẻ

a) \(\dfrac{2}{x+1}\) xác định với x≠-1, \(\sqrt{x+3}\) xác định với x ≥ -3
Tập xác định của y = là:
D = {x ∈ R/ x + 1 ≠ 0 và x + 3 ≥ 0} = [-3, +∞)\{-1}
Có thể viết cách khác: D = [-3, -1] ∪ (-1, +∞)
b) Tập xác định
D = {x ∈ R/ 2 -3x ≥ 0} ∩ {x ∈ R/ 1-2x ≥ 0}
= [-∞, 2323 ]∩(-∞, 1212) = (-∞, 1212)
c) Tập xác định là:
D = [1, +∞) ∪ (-∞,1) = R

a) TXĐ: \(D=R\).
b) \(TXD=D=R\backslash\left\{4\right\}\)
c) Đkxđ: \(\left\{{}\begin{matrix}4x+1\ge0\\-2x+1\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{-1}{4}\\x\le\dfrac{1}{2}\end{matrix}\right.\) \(\Leftrightarrow\dfrac{-1}{4}\le x\le\dfrac{1}{2}\).
TXĐ: D = \(\left[\dfrac{-1}{4};\dfrac{1}{2}\right]\)
a) Đkxđ: \(\left\{{}\begin{matrix}x+9\ge0\\x^2+8x-20\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge-9\\\left\{{}\begin{matrix}x\ne2\\x\ne-10\end{matrix}\right.\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-9\\x\ne2\end{matrix}\right.\)
Txđ: D = [ - 9; 2) \(\cup\) \(\left(2;+\infty\right)\)
b) Đkxđ: \(\left\{{}\begin{matrix}2x+1\ne0\\x-3\ne0\end{matrix}\right.\Leftrightarrow\Leftrightarrow\left\{{}\begin{matrix}x\ne\dfrac{-1}{2}\\x\ne3\end{matrix}\right.\)
Txđ: \(D=R\backslash\left\{\dfrac{-1}{2};3\right\}\)
c) \(x^2+2x-5\ne0\Leftrightarrow\left\{{}\begin{matrix}x\ne-1+\sqrt{6}\\x\ne-1-\sqrt{6}\end{matrix}\right.\)
Txđ: \(D=R\backslash\left\{-1+\sqrt{6};-1-\sqrt{6}\right\}\)

a) Tập xác định của y = f(x) = |x| là D = R.
∀x ∈ R => -x ∈ R
f(- x) = |- x| = |x| = f(x)
Vậy hàm số y = |x| là hàm số chẵn.
b) Tập xác định của
y = f(x) = (x + 2)2 là R.
x ∈ R => -x ∈ R
f(- x) = (- x + 2)2 = x2 – 4x + 4 ≠ f(x)
f(- x) ≠ - f(x) = - x2 – 4x - 4
Vậy hàm số y = (x + 2)2 không chẵn, không lẻ.
c) D = R, x ∈ D => -x ∈ D
f(– x) = (– x3) + (– x) = - (x3 + x) = – f(x)
Vậy hàm số đã cho là hàm số lẻ.
d) Hàm số không chẵn cũng không lẻ.

ĐKXĐ: 1+x>=0 và 1-x>=0
=>x>=-1 và x<=1
=>-1<=x<=1
\(f\left(-x\right)=\dfrac{\sqrt{1-x}-\sqrt{1+x}}{\left|-x+2\right|-\left|-x-2\right|}=-f\left(x\right)\)
=>f(x) là hàm số lẻ

a) Tập xác định của f(x) :
A = {x ∈ R | x2 + 3x + 4 ≥ 0 và -x2 + 8x – 15 ≥ 0}
- x2 + 3x + 4 có biệt thức Δ = 32 – 16 < 0
Theo định lí dấu của tam thức:
x2 + 3x + 4 ≥ 0 ∀x ∈R
-x2 + 8x – 15 = 0 ⇔ x1 = 3, x2 = 5
-x2 + 8x – 15 > 0 ⇔ 3 ≤ x ≤ 5 ⇒ A = [3, 5]
b) A/B = [3, 4]
R\(A\B) = (-∞, 3) ∪ (4, +∞)

a/ \(f\left(-x\right)=-x^3+2x^2-1\) hàm ko chẵn ko lẻ
b/ TXĐ: \(x\ge-1\) không phải 1 miền đối xứng nên hàm ko chẵn ko lẻ
c/ \(f\left(-x\right)=\left|-x-2\right|=\left|x+2\right|\) hàm vẫn ko chẵn ko lẻ
d/ TXĐ của hàm là đối xứng
\(f\left(-x\right)=\frac{\left|-x-2\right|+\left|-x+2\right|}{\left|-x\right|}=\frac{\left|x+2\right|+\left|x-2\right|}{\left|x\right|}=f\left(x\right)\)
Hàm chẵn
a/ f(−x)=−x3+2x2−1f(−x)=−x3+2x2−1 hàm ko chẵn ko lẻ
b/ TXĐ: x≥−1x≥−1 không phải 1 miền đối xứng nên hàm ko chẵn ko lẻ
c/ f(−x)=|−x−2|=|x+2|f(−x)=|−x−2|=|x+2| hàm vẫn ko chẵn ko lẻ
d/ TXĐ của hàm là đối xứng
f(−x)=|−x−2|+|−x+2||−x|=|x+2|+|x−2||x|=f(x)f(−x)=|−x−2|+|−x+2||−x|=|x+2|+|x−2||x|=f(x)
Hàm chẵn

a) \(D=(0;+\infty)\backslash\left\{1\right\}\)
b) \(D=[2;+\infty)\)

a: 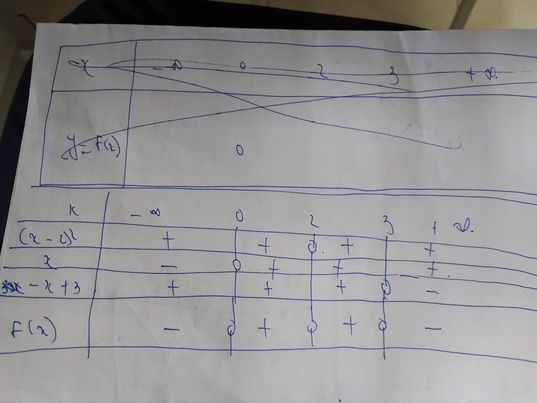
b: 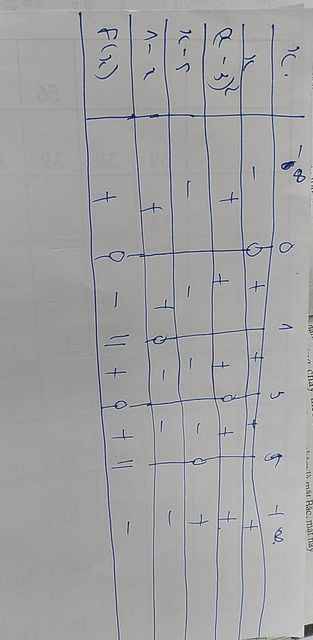
c: Đặt f(x)=0
=>-x^2+x+6=0
=>x^2-x-6=0
=>x=3 hoặc x=-2
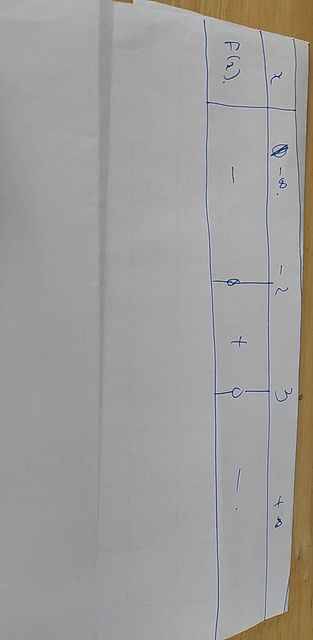
d: 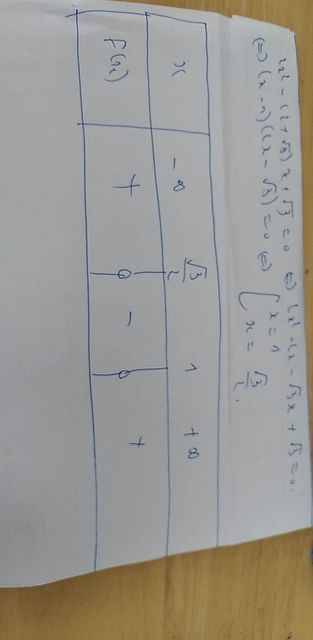
a, Ta có : \(f\left(x\right)=\left[{}\begin{matrix}x.x=x^2\\x\left(-x\right)=-x^2\end{matrix}\right.\)
=> Hàm f(x) là hàm chẵn .
b, Ta có : \(f\left(x\right)-f\left(-x\right)=\dfrac{\sqrt{1-x^2}}{x^3+x}+\dfrac{\sqrt{1-x^2}}{x^3+x}\ne0\)
\(\Rightarrow f\left(x\right)\ne f\left(-x\right)\)
=> Hàm f(x) là hàm lẻ .
Ủa gì ngộ vậy,ai làm kiểu này bao giờ?
a)\(D=R\)\(\Rightarrow\forall x\in D\) thì \(-x\in D\)
Có \(f\left(-x\right)=-x\left|-x\right|=-x\left|x\right|=-f\left(x\right)\)
\(\Rightarrow f\left(x\right)\) là hàm lẻ
b)\(D=R\backslash\left\{0\right\}\)\(\Rightarrow\forall x\in D\) thì \(-x\in D\)
Có \(f\left(-x\right)=\dfrac{\sqrt{1-\left(-x\right)^2}}{\left(-x\right)^3+\left(-x\right)}=-\dfrac{\sqrt{1-x^2}}{x^3+x}=-f\left(x\right)\)
\(\Rightarrow f\left(x\right)\) là hàm lẻ