Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Với \(m=1;n=\sqrt{2}\)thay vào phương trình ta có
\(x^2+\left(\sqrt{2}+1\right)x+\sqrt{2}=0\Leftrightarrow x\left(x+\sqrt{2}\right)+\left(x+\sqrt{2}\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x+\sqrt{2}\right)=0\Leftrightarrow\orbr{\begin{cases}x=-1\\x=-\sqrt{2}\end{cases}}\)
Vậy với \(m=1;n=\sqrt{2}\)thì phương trình có 2 nghiệm \(x=-1;x=-\sqrt{2}\)
b. Ta có \(\Delta=\left(mn+1\right)^2-4mn=m^2n^2+2mn+1-4mn=m^2n^2-2mn+1\)
\(=\left(mn-1\right)^2>0\forall m,n\)
Vậy phương trình luôn có 2 nghiệm phân biệt với mọi m;n

a) Thay x=-3 vào phương trình 2x2 – m2x +18m =0 ta được:
2(-3)2 - m2(-3) + 18m =0 ⇔ 3m2 +18m+18 =0
⇔ m2 + 6m +6 = 0
Δ' = 32 -1.6 = 9 -6 =3 > 0
√Δ' = √3
Phương trình có 2 nghiệm phân biệt:
Vậy với m=3 - 3 hoặc m=- 3- 3 thì phương trình đã cho có nghiệm x= -3
b) Thay x = -2 vào phương trình mx2 – x – 5m2 = 0 ta được:
m(-2)2 – (-2) – 5m2=0 ⇔ 5m2 – 4m -2 =0
Δ' = (-2)2 -5.(-2) = 4+10 = 14 > 0
√Δ' = √14
Phương trình có 2 nghiệm phân biệt:

b/ \(\hept{\begin{cases}x^2+px+1=0\\x^2+qx+1=0\end{cases}}\)
Theo vi et ta có
\(\hept{\begin{cases}a+b=-p\\ab=1\end{cases}}\) và \(\hept{\begin{cases}c+d=-q\\cd=1\end{cases}}\)
Ta có: \(\left(a-c\right)\left(b-c\right)\left(a-d\right)\left(b-d\right)\)
\(=\left(c^2-c\left(a+b\right)+ab\right)\left(d^2-d\left(a+b\right)+ab\right)\)
\(=\left(c^2+cp+1\right)\left(d^2+dp+1\right)\)
\(=cdp^2+pcd\left(c+d\right)+p\left(c+d\right)+c^2d^2+\left(c+d\right)^2-2cd+1\)
\(=p^2-pq-pq+1+q^2-2+1\)
\(=p^2-2pq+q^2=\left(p-q\right)^2\)
a/ \(\hept{\begin{cases}x^2+2mx+mn-1=0\left(1\right)\\x^2-2nx+m+n=0\left(2\right)\end{cases}}\)
Ta có: \(\Delta'_1+\Delta'_2=\left(m^2-mn+1\right)+\left(n^2-m-n\right)\)
\(=m^2+n^2-mn-m-n+1\)
\(=\left(\frac{m^2}{2}-mn+\frac{n^2}{2}\right)+\left(\frac{m^2}{2}-m+\frac{1}{2}\right)+\left(\frac{n^2}{2}-n+\frac{1}{2}\right)\)
\(=\frac{1}{2}\left(\left(m-n\right)^2+\left(m-1\right)^2+\left(n-1\right)^2\right)\ge0\)
Vậy có 1 trong 2 phương trình có nghiệm
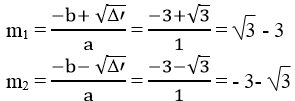



Gọi \(\Delta_1\)là biệt thức của pt \(x^2+mx+n=0\)
\(\Delta_2\)là biệt thức của pt \(x^2-2x-n=0\)
Ta có : \(\Delta_1+\Delta_2=\left(m^2-4n\right)+\left(4+4n\right)\)
\(=m^2+4>0\forall m\)
Nên tồn tại 1 trong 2 delta phải lớn hơn 0
=> 1 trong 2 pt đã cho có nghiệm với mọi m và n
Vậy .......