Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt \(\left\{{}\begin{matrix}\sqrt{a-1}=x\\\sqrt{b-1}=y\\\sqrt{c-1}=z\end{matrix}\right.\) thì BĐT cần chứng minh trở thành:
\(\sqrt{\left(x^2+1\right)\left(y^2+1\right)\left(z^2+1\right)+z^2+1}\ge x+y+z\)
\(\Leftrightarrow\left(x^2+1\right)\left(y^2+1\right)\left(z^2+1\right)+z^2+1\ge\left(x+y+z\right)^2\)
\(\Leftrightarrow x^2y^2z^2+x^2y^2+y^2z^2+z^2x^2-2xy-2yz-2zx+z^2+2\ge0\)
\(\Leftrightarrow\left(x^2y^2z^2+z^2-2xyz^2\right)+\left(x^2z^2+y^2z^2+2xyz^2\right)-2z\left(x+y\right)+1+\left(x^2y^2-2xy+1\right)\ge0\)
\(\Leftrightarrow\left(xyz-z\right)^2+\left(xz+yz\right)^2-2\left(xz+yz\right)+1+\left(xy-1\right)^2\ge0\)
\(\Leftrightarrow\left(xyz-z\right)^2+\left(xz+yz-1\right)^2+\left(xy-1\right)^2\ge0\) (luôn đúng)
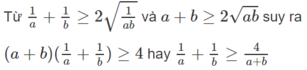
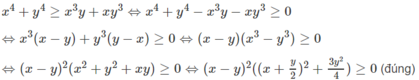
Đáp án :
In\(\frac{7}{3}\)
.... hok tốt !
Cám ơn bạn