Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án: C.
Gọi N là số hạt nhân U238 hiện tại, N0 là số hạt U238 lúc đầu
Khi đó N0 = N + ∆ N = N + NPb (Vì một hạt nhân U238 sau khi phân rã tạo thành một hạt Pb206)
Theo ĐL phóng xạ: 
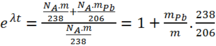= 1,0525 → t = 3,3.108 năm.
Khối lượng còn lại của hai đồng vị sau thời gian t là
\(m(238) = m_{0238}.2^{-t/T_1}.\\ m(235) = m_{0235}.2^{-t/T_2}.\)
Chi hai phương trình ta thu được
\(\frac{m(238)}{m(235)} = 2^{t(\frac{1}{T_2}-\frac{1}{T_1})}.(2)\)
mà hiện tại tỉ số khối lượng của chúng là \(\frac{92,848}{7,142} = 13.\)
Thay vào phương trình (2) ta được \(2^{t(1/T_2-1/T_1)} = 13 => t (1/T_2-1/T_1) = \ln_2{13} => t \approx 3,1.10^9\) năm.
Vậy tuổi Trái Đất cỡ 3,1 tỷ năm.
Cứ 1 hạt nhân \(_{92}^{238}U\) bị phân rã tạo ra 1 hạt nhân \(_{82}^{206}Pb\). Từ đó ta có nhận xét là số hạt nhân \(_{92}^{238}U\) bị phân rã chính bằng số hạt nhân \(_{82}^{206}Pb\) tạo thành.
Tỉ số giữa số hạt nhân \(_{92}^{238}U\) bị phân rã và số hạt nhân \(_{92}^{238}U\) còn lại là
\(\frac{\Delta N}{N}= \frac{6,239.10^{18}}{1,188.10^{20}}= 0,0525 = \frac{1-2^{-\frac{t}{T}}}{2^{-\frac{t}{T}}}\)
Nhân chéo => \(2^{-\frac{t}{T}}= 0,95.\)
=> \(t = -T\ln_2 0,95 = 3,3.10^8\)(năm)
=> Tuổi của khối đã là 3,3.108 năm.
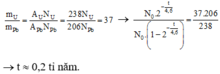
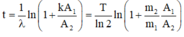
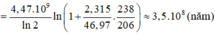
Khối lượng Urani 238 còn lại sau thời gian t là
\(m_{238} = m_0.2^{-t/T_1}.(1)\)
Cứ 1 hạt Urani phân rã sẽ tạo thành 1 hạt Pb.
Như vậy số hạt Urani bị phân rã chính là số hạt Pb hình thành. Gọi \(\Delta m\) (Urani) là khối lượng Urani đã bị phân rã
Khối lượng Pb hình thành là
\(m_{Pb} = n_{pB}.M_{Pb} = \frac{\Delta m_{Urani}}{M_{urani}}.M_{Pb} \)
=> \(\Delta m_{Urani}= \frac{4,27.10^{-5}}{206}.238 = 4,933.10^{-5}kg.\)
Ta lại có
=> \(\Delta m = m_0 - m(t) = m(t).2^{t/T}-m(t) = m(t).(2^{t/T}-1).\)
=> \(4,933.10^{-5} = 93,94.10^{-5}.(2^{t/T}-1) \)
=> \(t = 3,3.10^8.\) năm.
Tuổi của khối đã là 3,3.108 năm.