Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

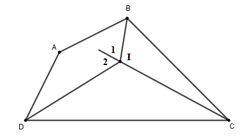
Gọi góc phân giác góc B, D là góc B1, D1
\(\Rightarrow\) \(\widehat{\text{B1}}\)=\(\dfrac{\widehat{B}}{2}\), \(\widehat{\text{D1}} =\dfrac{\widehat{D}}{2}\)
Trong tứ giác ABID, có góc \(\widehat{\text{A}}+\widehat{B1}+\widehat{ BID}+\widehat{\text{D1}}\)=360
\(\Leftrightarrow\)\(\widehat{\text{A}}+\widehat{\dfrac{B}{2}}+\widehat{BID}+\dfrac{\widehat{\text{D}}}{2}\)=3600
\(\Leftrightarrow\)\(2\widehat{\text{A}}+\widehat{B}+\widehat{2BID}+\widehat{2\text{D}}\)=3600.2
\(\Leftrightarrow\) \(\widehat{B}+\widehat{D}\)= 720- \(2\widehat{\text{A}}+\widehat{2BID}\) (1)
Trong tứ giác ABCD ta có: \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{\text{D}}\)=3600 (2)
Mà \(\widehat{A}-\widehat{C}\)=600
\(\Leftrightarrow\) A=60+C thay vào (2):\(60^0+\widehat{2C}+\widehat{B}+\widehat{D}=360^0\) (3)
Thay 1 vào 3, ta có: \(60^0+\widehat{2C}+720-2\widehat{A}+\widehat{2BID}=360^0\)
\(\Leftrightarrow\)600+7200 - 2.600-3600= \(\widehat{2BID}\)
\(\Leftrightarrow\) \(\widehat{2BID}\)= 1500

A B C D O 1 2 3 4
Có : \(AB< OA+OB;BC< OB+OC;CD< OC+OD;DA< OD+OA\)
\(P_{ABCD}=2p=AB+BC+CD+DA< 2\left(OA+OB+OC+OD\right)\)
\(\Leftrightarrow\)\(p< OA+OB+OC+OD\)
Lại có : \(OA< AB-OB;OB< BC-OC;OC< CD-OD;OD< DA-OA\)
Cộng vế theo vế từng bđt trên ta được :
\(OA+OB+OC+OD< AB+BC+CD+DA-\left(OA+OB+OC+OD\right)\)
\(\Leftrightarrow\)\(2\left(OA+OB+OC+OD\right)< AB+BC+CD+DA\) (*)
Có tiếp -,- :
\(OA< AB+OB;OA< DA+OD\)\(\Rightarrow\)\(2OA< AB+DA+OB+OD\)
\(OB< AB+OA;OB< BC+OC\)\(\Rightarrow\)\(2OB< AB+BC+OA+OC\)
\(OC< BC+OB;OC< CD+OD\)\(\Rightarrow\)\(2OC< BC+CD+OB+OD\)
\(OD< CD+OC;OD< DA+OA\)\(\Rightarrow\)\(2OD< CD+DA+OC+OA\)
\(\Rightarrow\)\(2\left(OA+OB+OC+OD\right)< 2\left(AB+BC+CD+DA\right)+2\left(OA+OB+OC+OD\right)\)
\(< 2\left(AB+BC+CD+DA\right)+\left(AB+BC+CD+DA\right)\) ( kết hợp với (*) )
\(\Rightarrow\)\(2\left(OA+OB+OC+OD\right)< 3\left(AB+BC+CD+DA\right)\)
\(\Leftrightarrow\)\(OA+OB+OC+OD< 3.\frac{AB+BC+CD+DA}{2}=3.\frac{2p}{2}=3p\)
Vậy \(p< OA+OB+OC+OD< 3p\)

a) từ I kẻ HI//AB//DC
=> GÓC HID= GÓC IDC ( SLT)
MÀ IDC=IDH => GÓC HID=GÓC IDH => TAM GIÁC HID CÂN TẠI H => HD=HI
TƯƠNG TỰ CHỨNG MINH TAM GIÁC HIA CÂN TẠI H => HI=HA
=> HA=HD => H LÀ TRUNG ĐIỂM AD
MÀ HI//AC//CD => I PHẢI LÀ TRUNG ĐIỂM BC
=> HI LÀ ĐTB CỦA HÌNH THANG
=> HI= (AB+CD)/2 (1)
MẶT KHÁC TRONG TAM GIÁC IAD:
GÓC ADI + GÓC IDA=1/2 GÓC A +1/2 GÓC D=1/2 (A+D)=1/2 180=90 ( ABCD LÀ HÌNH THANG => A+D=180)
=> TAM GIÁC ADI VUÔNG TẠI I. HI LÀ TRUNG TUYẾN => HI=AD/2 (2)
TỪ (1;2) => ĐPCM
B) GỌI PG GÓC A CẮT PG GÓC D TẠI I
TỪ I TA KẺ HI//AB//CD (H THUỘC AD)
=> .... ( ĐẾN ĐÂY C/M NHƯ TRÊN ĐỂ => H LÀ TĐ CỦA AD, TAM GIÁC ADI VUÔNG)
=> HI= AD/2.
TA CÓ: AD=AB+CD => HI=AB+CD/2 HAY HI= NỬA TỔNG 2 ĐÁY
H LÀ TRUNG ĐIỂM AD, HI//AB//CD. HI = NỬA TỔNG HAI ĐÁY => I PHẢI LÀ TRUNG ĐIỂM BC => AI CẮT DI TẠI I THUỘC BC