Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Gọi E, F lần lượt là giao điểm của AM và CD, BN và CD
Ta có : AB//CD (gt) => E = A1 (so le trong)
Mà A1 =A2 (gt)
Nên A2 = E
Xét ΔADE cân tại D, có DM là p/giác nên DM đồng thời là trung tuyến
=>AM= EM
Chứng minh tương tự, ta được :
BN = FN
Xét hình thang ABEF có : AM=BN(cm trên)
BN=FN(cm trên)
Do đó MN là đường TB của HÌNH thang ABEF
=> MN= \(\frac{EF+AB}{2}\)
MN//AB//EF Vậy MN// CD(đpcm)
b)Do ED= AD; BC=FC
Mà ED + DC + CF = EF
Nên AD + DC + BC = EF
Lại có MN \(\frac{EF+AB}{2}\)(CM trên)
Suy ra MN= \(\frac{AD+DC+BC+AB}{2}\)\(=\frac{a+b+c+d}{2}\)

a. Gọi M' và N' là giao điểm của tia AM và BN với CD.
Ta có: ∠(M') = ∠A2(sole trong)
∠A1= ∠A2(gt)
⇒ ∠(M') = ∠A1nên ΔADM' cân tại D
* DM là phân giác của ∠(ADM' )
Suy ra: DM là đường trung tuyến (tính chất tam giác cân)
⇒ AM = MM'
∠(N') = ∠B1nên ΔBCN' cân tại C.
* CN là phân giác của ∠(BCN')
Suy ra: CN là đường trung tuyến (tính chất tam giác cân)
⇒ PN = NN'
Suy ra: MN là đường trung bình của hình thang ABN'M'
⇒ MN = M'N' (tính chất đường trung hình hình thang)
Hay MN//CD
b)MN=AB+M′N′/2 (tính chất đường trung bình của hình thang)
⇒MN=AB+M′D+CD+CN′/2(1)
Mà M′D=AD,CN′=BC. Thay vào (1)
MN=AB+AD+CD+BC/2=a+d+c+b/2

xet tam giac ADM có
gocDAM=1/2 goc ngoai tai A
gocADM=1/2goc ngoai tai D
cong lai:gocADM+gocDAM=90*=> tam giac ADM vuông tại M
tương tự tam giac BNC vuông tại N
keo dai AM va` BN cắt CD tại E,F
xet tam giac ADE co DM vừa la` đường cao vừa la` phân giác => tam giac ADE can tai D=>DM la` trung tuyến =>M la` trung điểm AE
tương tự N la` trung diem BF
=> MN la` đuơng trung binh cua hinh thang AEFB =>MN//CD

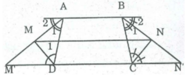
Gọi M' và N' là giao điểm của tia AM và BN với CD.
Ta có: ∠ (M') = ∠ A 2 (sole trong)
∠ A 1 = ∠ A 2 (gt)
⇒ ∠ (M') = ∠ A 1 nên ∆ ADM' cân tại D
* DM là phân giác của ∠ (ADM' )
Suy ra: DM là đường trung tuyến (tính chất tam giác cân)
⇒ AM = MM'
∠ (N') = ∠ B 1 nên ∆ BCN' cân tại C.
* CN là phân giác của ∠ (BCN')
Suy ra: CN là đường trung tuyến (tính chất tam giác cân)
⇒ BN = NN'
Suy ra: MN là đường trung bình của hình thang ABN'M'
⇒ MN // M'N' (tính chất đường trung hình hình thang)
Hay MN//CD

a:
góc AMD=180 độ-góc MAD-góc MDA
\(=180^0-\dfrac{180^0-\widehat{BAD}}{2}-\dfrac{180^0-\widehat{ADC}}{2}\)
\(=180^0-\dfrac{1}{2}\widehat{ADC}-90^0+\dfrac{1}{2}\widehat{ADC}=90^0\)
Gọi giao của AM với DC là M'
Xét ΔDM'A có
DM là đường cao, là đường phân giác
nên ΔDM'A cân tại D
=>M là trung điểm của AM'
Gọi giao của BN với DC là N'
Ta có: \(\widehat{BNC}=180^0-\widehat{NBC}-\widehat{NCB}\)
\(=180^0-\dfrac{180^0-\widehat{ABC}}{2}-\dfrac{180^0-\widehat{BCD}}{2}\)
\(=180^0-90^0+\dfrac{1}{2}\widehat{ABC}-90^0+\dfrac{1}{2}\widehat{BCD}\)
=90 độ
Xét ΔCN'B có
CN vừa là đường cao, vừa là phân giác
nên ΔCN'B cân tại C
=>N là trug điểm của BN'
Xét hình thang ABN'M' có
M,N lần lượt là trung điểm của AM' và BN'
nen MN là đường trung bình
=>MN//CD//AB
b: MN=(AB+M'N')/2
=(AB+M'D+CD+CN')/2
mà M'D=AD và CN'=CB
nên MN=(AB+CD+AD+CB)/2
