Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

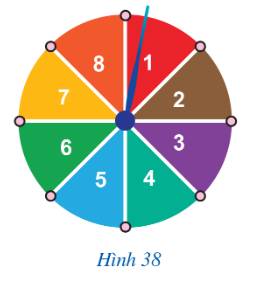
Số kết quả có thể xảy ra là: 8
Tập hợp các kết quả thuận lợi của biến cố “Mũi tên chỉ vào hình quạt ghi số nhỏ hơn 6” là:
\(A = \left\{ {1;2;3;4;5} \right\}\)
Số kết quả thuận lợi là 5
Vì thế, xác suất của biến cố đó là: \(\frac{5}{8}\)

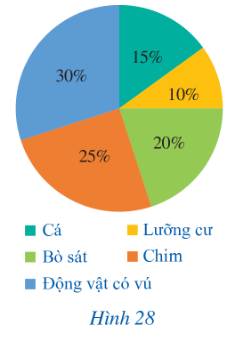
Dựa vào biểu đồ quạt tròn, ta có bảng thống kê sau:
Lớp động vật có xương sống | Cá | Lưỡng cư | Bò sát | Chim | Động vật có vú |
Tỉ lệ mẫu vật (%) | 15 | 10 | 20 | 25 | 30 |

a)
Mức vé | A | B | C | D |
Tỉ lệ vé (%) | 35 | 45 | 15 | 5 |
b) Mỗi hình quạt tương ứng với 5% nên ta có:
Tỉ lệ vé mức A (35%) ứng với 7 hình quạt tròn.
Tỉ lệ vé mức B (45%) ứng với 9 hình quạt tròn.
Tỉ lệ vé mức C (15%) ứng với 3 hình quạt tròn.
Tỉ lệ vé mức D (5%) ứng với 1 hình quạt tròn.


a) 3,27 tỉ đô la Mỹ = 3270 triệu đô la Mỹ
Kim ngạch xuất khẩu rau quả sang Trung Quốc là:
\(3720.56,3\% \approx 1841\) (triệu đô la Mỹ)
Kim ngạch xuất khẩu rau quả sang ASEAN là:
\(3270.8,8\% = 287,8\) (triệu đô la Mỹ)
Kim ngạch xuất khẩu rau quả sang Mỹ là:
\(3,27.5,2\% \approx 170\) (triệu đô la Mỹ)
Kim ngạch xuất khẩu rau quả sang EU là:
\(3,27.4,5\% \approx 147,2\) (triệu đô la Mỹ)
Kim ngạch xuất khẩu rau quả sang Hàn Quốc là:
\(3,27.4,4\% \approx 143,9\) (triệu đô la Mỹ)
Kim ngạch xuất khẩu rau quả sang Nhật Bản là:
\(3,27.3,9\% \approx 127,5\) (triệu đô la Mỹ)
Kim ngạch xuất khẩu rau quả sang các thị trường khác là:
\(3,27.16,9\% \approx 552,6\) (triệu đô la Mỹ)
Ta có bảng thống kê:
Thị trường xuất khẩu | Trung Quốc | ASEAN | Mỹ | EU | Hàn Quốc | Nhật Bản | Khác |
Kim ngạch xuất khẩu rau quả (triệu đô la Mỹ) | 1841 | 287,8 | 170 | 147,2 | 143,9 | 127,5 | 552,6 |
b) Tổng kim ngạch xuất khẩu sang các thị trường còn loại ngoài Trung Quốc là:
\(287,8 + 170 + 147,2 + 143,9 + 127,5 + 552,6 = 1429\) (triệu đô la Mỹ)
Kim ngạch xuất khẩu rau quả sang thị trường Trung Quốc nhiều hơn các thị trường còn lại số triệu đô la Mỹ là:
\(1841 - 1429 = 412\) (triệu đô la Mỹ)

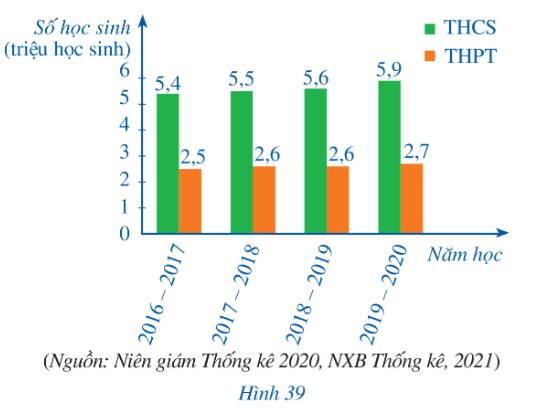
a)
Năm học | 2016 - 2017 | 2017 - 2018 | 2018 - 2019 | 2019 – 2020 |
Số học sinh THCS | 5,4 | 5,5 | 5,6 | 5,9 |
Số học sinh THPT | 2,5 | 2,6 | 2,6 | 2,7 |
b)
Tỉ số của số học sinh THCS và số học sinh THPT trong năm 2016 – 2017 là: \(\frac{{5,4}}{{2,5}} \approx 2,2\)
Tỉ số của số học sinh THCS và số học sinh THPT trong năm 2017 – 2018 là: \(\frac{{5,5}}{{2,6}} \approx 2,1\)
Tỉ số của số học sinh THCS và số học sinh THPT trong năm 2018 – 2019 là: \(\frac{{5,6}}{{2,6}} \approx 2,2\)
Tỉ số của số học sinh THCS và số học sinh THPT trong năm 2019 – 2020 là: \(\frac{{5,9}}{{2,7}} \approx 2,2\)
Ta có bảng:
Năm học | 2016 - 2017 | 2017 - 2018 | 2018 - 2019 | 2019 – 2020 |
Tỉ số của số học sinh THCS và số học sinh THPT | 2,2 | 2,1 | 2,2 | 2,2 |
c) Trong Bảng 1, ta thấy rằng tỉ số của số học sinh THCS và số học sinh THPT qua các năm học gần như là không thay đổi. Điều này cho thấy số lượng học sinh tham gia học THCS và THPT trong các năm khá ổn định, không có quá nhiều sự biến đổi.

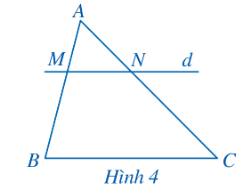
Xét tam giác ABC với \(MN\parallel BC\), ta có \(\frac{{MB}}{{AB}} = \frac{{NC}}{{AC}}\) (định lý Thales).

\({x^6} + {y^6} = {\left( {{x^2}} \right)^3} + {\left( {{y^2}} \right)^3} = \left( {{x^2} + {y^2}} \right)\left[ {{{\left( {{x^2}} \right)}^2} - {x^2}.{y^2} + {{\left( {{y^2}} \right)}^2}} \right] = \left( {{x^2} + {y^2}} \right)\left( {{x^4} - {x^2}{y^2} + {y^4}} \right)\)

a) Các trường hợp có thể xảy ra đối với số ghi ở hình quạt mà mũi tên chỉ vào đĩa khi dừng lại là: mũi tên chỉ số 1, mũi tên chỉ số 2, mũi tên chỉ số 3, mũi tên chỉ số 4, mũi tên chỉ số 5, mũi tên chỉ số 6, mũi tên chỉ số 7, mũi tên chỉ số 8.
\(C = \left\{ {1;2;3;4;5;6;7;8} \right\}\)
b) Các kết quả có thể xảy ra đối với biến cố D: “Mũi tên chỉ vào hình quạt ghi số lẻ” là: mũi tên chỉ số 1, mũi tên chỉ số 3, mũi tên chỉ số 5, mũi tên chỉ số 7.
\(D = \left\{ {1;3;5;7} \right\}\)
Các phần tử 1; 3; 5; 7 được gọi là kết quả thuận lợi cho biến cố D.
c) Số kết quả thuận lợi cho biến cố D là: 4
Số phần tử của tập hợp C là: 8
Tỉ số của số các kết quả thuận lợi cho biến cố D và số phần tử của tập hợp C là: \(\frac{4}{8} = \frac{1}{2}\) mũi tên

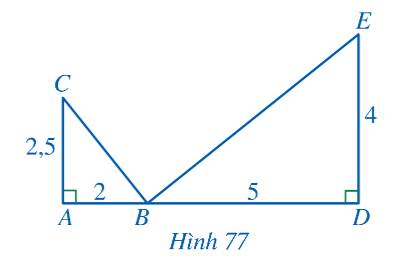
a) Ta thấy \(\frac{{AB}}{{DE}} = \frac{2}{4} = \frac{1}{2};\,\,\frac{{AC}}{{DB}} = \frac{2,5}{5} = \frac{1}{2}\)
\( \Rightarrow \frac{{AB}}{{DE}} = \frac{{AC}}{{DB}}\)
Xét tam giác ABC và tam giác DEB có:
\(\frac{{AB}}{{DE}} = \frac{{AC}}{{DB}}\) và \(\widehat {CAB} = \widehat {BDE} = 90^\circ \)
\( \Rightarrow \Delta ABC \backsim \Delta DEB\) (c-g-c)
\( \Rightarrow \widehat {ABC} = \widehat {BED}\)
b) Vì \(\Delta ABC \backsim \Delta DEB\) nên \(\widehat {ACB} = \widehat {DBE}\)
Mà tam giác ABC vuông tại A nên \(\widehat {ACB} + \widehat {ABC} = 90^\circ \) hay \(\widehat {DBE} + \widehat {ABC} = 90^\circ \)
Ta thấy
\(\begin{array}{l}\widehat {DBE} + \widehat {CBE} + \widehat {ABC} = 180^\circ \\ \Rightarrow \widehat {CBE} + 90^\circ = 180^\circ \\ \Rightarrow \widehat {CBE} = 90^\circ \end{array}\)
Vậy \(BC \bot BE\).
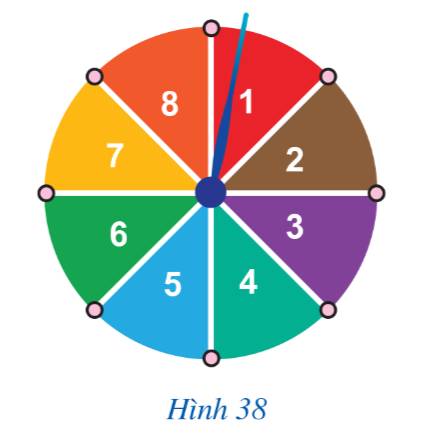







a) Có 8 kết quả có thể xảy ra là : 1; 2; 3; 4; 5; 6; 7; 8.
Có 2 kết quả thuận lợi của biến cố "Chiếc kim chỉ vào hình quạt ghi số chia cho 4 dư 3" là: 3; 7.
Xác suất của biến cố "Chiếc kim chỉ vào hình quạt ghi số chia cho 4 dư 3" là: \(\frac{2}{8} = \frac{1}{4}\).
b) Có 6 kết quả thuận lợi của biến cố "Chiếc kim chỉ vào hình quạt ghi số chỉ có đúng một ước nguyên tố" là: 2; 3; 4; 5; 7; 8.
Xác suất của biến cố "Chiếc kim chỉ vào hình quạt ghi số chỉ có đúng một ước nguyên tố" là: \(\frac{6}{8} = \frac{3}{4}\).