K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HQ
Hà Quang Minh
Giáo viên
11 tháng 1 2024
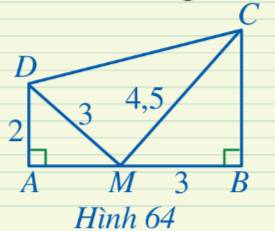
Vì \(\frac{{AD}}{{BM}} = \frac{2}{3},\,\,\frac{{DM}}{{MC}} = \frac{3}{{4,5}} = \frac{2}{3}\) nên \(\frac{{AD}}{{BM}} = \frac{{DM}}{{MC}}\).
Xét hai tam giác \(ADM\) và \(BMC\) có \(\widehat {MAD} = \widehat {CBM} = 90^\circ \) và \(\frac{{AD}}{{BM}} = \frac{{DM}}{{MC}}\) nên \(\Delta{ADM} \backsim \Delta{BMC}\).
Suy ra \(\widehat {AMD} = \widehat {BCM}\) và \(\widehat {ADM} = \widehat {BMC}\).
Xét tam giác \(ADM\) vuông tại A có:
\(\begin{array}{l}\,\,\,\,\,\,\,\,\widehat {AMD} + \widehat {ADM} = 90^\circ \\ \Rightarrow \widehat {AMD} + \widehat {BMC} = 90^\circ \end{array}\)
Mà ta có:
\(\begin{array}{l}\,\,\,\,\,\widehat {AMD} + \widehat {DMC} + \widehat {CMB} = 180^\circ \\ \Rightarrow 90^\circ + \widehat {DMC} = 180^\circ \\ \Rightarrow \widehat {DMC} = 90^\circ \end{array}\)
Vậy tam giác \(CDM\) vuông tại \(M\).
B
1
HQ
Hà Quang Minh
Giáo viên
12 tháng 1 2024
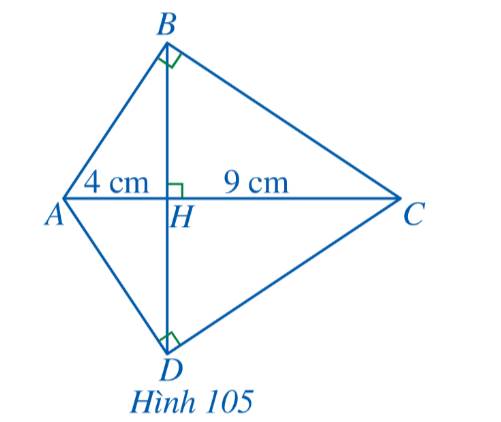
a) Xét tam giác ABC vuông tại B có: \(\widehat {BAC} + \widehat {BCA} = 90^\circ \)
Xét tam giác BHC vuông tại H có:
\(\begin{array}{l}\widehat {HBC} + \widehat {HCB} = 90^\circ \\ \Rightarrow \widehat {HBC} + \widehat {BCA} = 90^\circ \end{array}\)
\( \Rightarrow \widehat {HBC} = \widehat {BAC}\) hay \(\widehat {HBC} = \widehat {BAH}\)
Xét tam giác HAB và tam giác HBC có:
\(\widehat {BAH} = \widehat {CBH}\) và \(\widehat {BHA} = \widehat {CHB} = 90^\circ \)
\( \Rightarrow \Delta HAB \backsim \Delta HBC\)
b) Vì \(\Delta HAB \backsim \Delta HBC\) nên
\(\begin{array}{l}\frac{{HA}}{{HB}} = \frac{{HB}}{{HC}}\\ \Rightarrow H{B^2} = HA.HC\\ \Rightarrow H{B^2} = 4.9 = 36\\ \Rightarrow HB = 6cm\end{array}\)
Ta chứng minh được \(\Delta HAD \backsim \Delta HDC\)
\(\begin{array}{l} \Rightarrow \frac{{HA}}{{HD}} = \frac{{HD}}{{HC}}\\ \Rightarrow H{D^2} = HA.HC\\ \Rightarrow H{D^2} = 4.9 = 36\\ \Rightarrow HD = 6cm\end{array}\)
Vậy \(HB = HD = 6cm\).
B
1
HQ
Hà Quang Minh
Giáo viên
11 tháng 1 2024
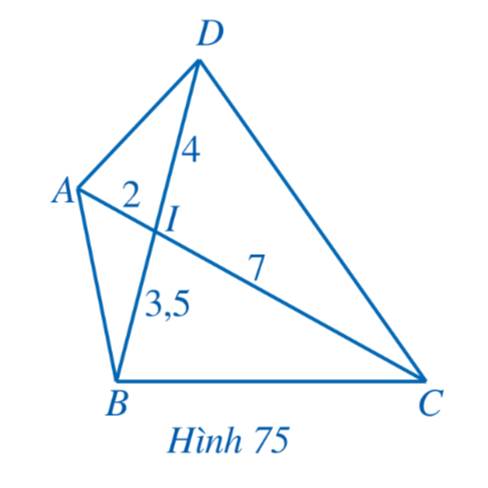
a) Ta thấy \(\frac{{IA}}{{ID}} = \frac{2}{4} = \frac{1}{2};\,\,\frac{{IB}}{{IC}} = \frac{3}{6} = \frac{1}{2}\)
\( \Rightarrow \frac{{IA}}{{ID}} = \frac{{IB}}{{IC}}\)
Mà \(\widehat {AIB} = \widehat {DIC}\) (hai góc đối đỉnh)
Xét tam giác IAB và tam giác IDC có:
\(\frac{{IA}}{{ID}} = \frac{{IB}}{{IC}}\) và \(\widehat {AIB} = \widehat {DIC}\)
\( \Rightarrow \)\(\Delta IAB \backsim \Delta IDC\) (c-g-c)
b) Ta thấy \(\frac{{IA}}{{IB}} = \frac{2}{3};\,\,\frac{{ID}}{{IC}} = \frac{4}{6} = \frac{2}{3}\)
\( \Rightarrow \frac{{IA}}{{IB}} = \frac{{ID}}{{IC}}\)
Mà \(\widehat {AID} = \widehat {BIC}\) (hai góc đối đỉnh)
Xét tam giác IAD và tam giác IBC có:
\(\frac{{IA}}{{IB}} = \frac{{ID}}{{IC}}\) và \(\widehat {AID} = \widehat {BIC}\)
\( \Rightarrow \)\(\Delta IAD \backsim \Delta IBC\) (c-g-c)
B
1
HQ
Hà Quang Minh
Giáo viên
11 tháng 1 2024
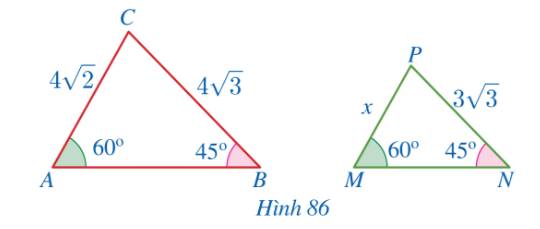
a) Xét tam giác ABC và tam giác MNP có:
\(\begin{array}{l}\widehat A = \widehat M = 60^\circ \\\widehat B = \widehat N = 45^\circ \end{array}\)
\( \Rightarrow \Delta ABC \backsim \Delta MNP\) (g-g)
b) Vì \(\Delta MNP \backsim \Delta ABC\) nên \(\frac{{AC}}{{MP}} = \frac{{BC}}{{NP}}\) (Tỉ số đồng dạng)
\(\begin{array}{l} \Rightarrow \frac{{4\sqrt 2 }}{x} = \frac{{4\sqrt 3 }}{{3\sqrt 3 }}\\ \Rightarrow x = \frac{{4\sqrt 2 .3\sqrt 3 }}{{4\sqrt 3 }} = 3\sqrt 2 \end{array}\)
HQ
Hà Quang Minh
Giáo viên
11 tháng 1 2024
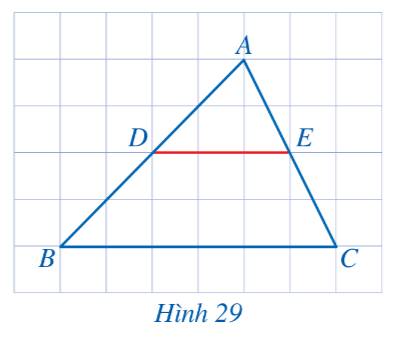
Quan sát hình ta thấy D và trung điểm của đoạn thẳng AB và E là trung điểm của đoạn thẳng AC.
B
1
HQ
Hà Quang Minh
Giáo viên
11 tháng 1 2024
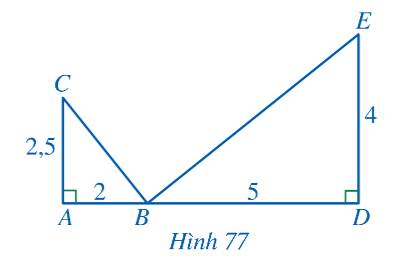
a) Ta thấy \(\frac{{AB}}{{DE}} = \frac{2}{4} = \frac{1}{2};\,\,\frac{{AC}}{{DB}} = \frac{2,5}{5} = \frac{1}{2}\)
\( \Rightarrow \frac{{AB}}{{DE}} = \frac{{AC}}{{DB}}\)
Xét tam giác ABC và tam giác DEB có:
\(\frac{{AB}}{{DE}} = \frac{{AC}}{{DB}}\) và \(\widehat {CAB} = \widehat {BDE} = 90^\circ \)
\( \Rightarrow \Delta ABC \backsim \Delta DEB\) (c-g-c)
\( \Rightarrow \widehat {ABC} = \widehat {BED}\)
b) Vì \(\Delta ABC \backsim \Delta DEB\) nên \(\widehat {ACB} = \widehat {DBE}\)
Mà tam giác ABC vuông tại A nên \(\widehat {ACB} + \widehat {ABC} = 90^\circ \) hay \(\widehat {DBE} + \widehat {ABC} = 90^\circ \)
Ta thấy
\(\begin{array}{l}\widehat {DBE} + \widehat {CBE} + \widehat {ABC} = 180^\circ \\ \Rightarrow \widehat {CBE} + 90^\circ = 180^\circ \\ \Rightarrow \widehat {CBE} = 90^\circ \end{array}\)
Vậy \(BC \bot BE\).
B
1
HQ
Hà Quang Minh
Giáo viên
12 tháng 1 2024
Học sinh thực hiện theo hướng dẫn của GV và SGK.
Ta có thể gấp và cắt giấy thành những chữ cái in hoa đồng dạng với nhau khác như:
B
1
HQ
Hà Quang Minh
Giáo viên
11 tháng 1 2024
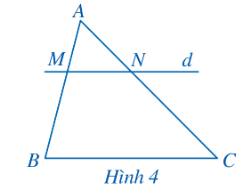
Xét tam giác ABC với \(MN\parallel BC\), ta có \(\frac{{MB}}{{AB}} = \frac{{NC}}{{AC}}\) (định lý Thales).
H9
HT.Phong (9A5)
CTVHS
23 tháng 1 2024
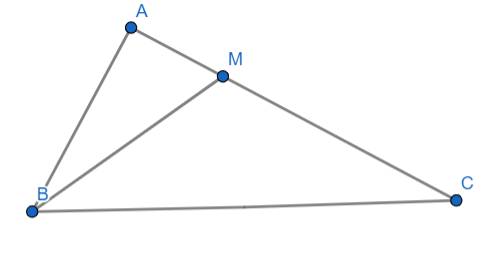
a) Áp dụng định lý Py-ta-go cho tam giác ABC vuông tại A ta có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow BC=\sqrt{AB^2+AC^2}\)
\(\Rightarrow BC=\sqrt{10^2+20^2}=10\sqrt{5}\left(cm\right)\)
Áp dụng định lý Py-ta-go cho tam giác ABM vuông tại A ta có:
\(BM^2=AB^2+AM^2\)
\(\Rightarrow BM=\sqrt{AB^2+AM^2}\)
\(\Rightarrow BM=\sqrt{10^2+5^2}=5\sqrt{5}\left(cm\right)\)
b) Ta có:
\(\dfrac{AM}{AB}=\dfrac{1}{2}\)
\(\dfrac{BM}{BC}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{AM}{AB}=\dfrac{MB}{BC}=\dfrac{1}{2}\)
Xét hai tam giác ABC và AMB có:
\(\widehat{BAC}\) chung
\(\dfrac{AM}{AB}=\dfrac{MB}{BC}=\dfrac{1}{2}\)
\(\Rightarrow\Delta ABC\sim\Delta AMB\left(c.g.c\right)\)
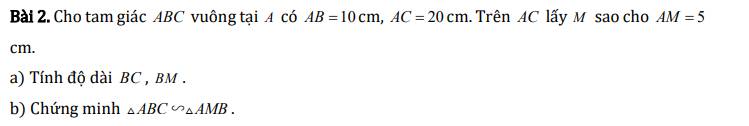
\({x^6} + {y^6} = {\left( {{x^2}} \right)^3} + {\left( {{y^2}} \right)^3} = \left( {{x^2} + {y^2}} \right)\left[ {{{\left( {{x^2}} \right)}^2} - {x^2}.{y^2} + {{\left( {{y^2}} \right)}^2}} \right] = \left( {{x^2} + {y^2}} \right)\left( {{x^4} - {x^2}{y^2} + {y^4}} \right)\)