Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

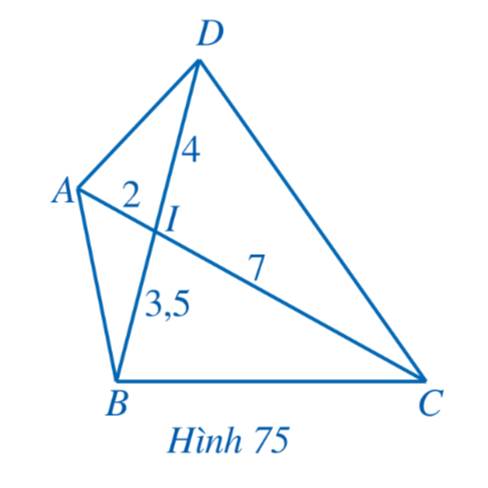
a) Ta thấy \(\frac{{IA}}{{ID}} = \frac{2}{4} = \frac{1}{2};\,\,\frac{{IB}}{{IC}} = \frac{3}{6} = \frac{1}{2}\)
\( \Rightarrow \frac{{IA}}{{ID}} = \frac{{IB}}{{IC}}\)
Mà \(\widehat {AIB} = \widehat {DIC}\) (hai góc đối đỉnh)
Xét tam giác IAB và tam giác IDC có:
\(\frac{{IA}}{{ID}} = \frac{{IB}}{{IC}}\) và \(\widehat {AIB} = \widehat {DIC}\)
\( \Rightarrow \)\(\Delta IAB \backsim \Delta IDC\) (c-g-c)
b) Ta thấy \(\frac{{IA}}{{IB}} = \frac{2}{3};\,\,\frac{{ID}}{{IC}} = \frac{4}{6} = \frac{2}{3}\)
\( \Rightarrow \frac{{IA}}{{IB}} = \frac{{ID}}{{IC}}\)
Mà \(\widehat {AID} = \widehat {BIC}\) (hai góc đối đỉnh)
Xét tam giác IAD và tam giác IBC có:
\(\frac{{IA}}{{IB}} = \frac{{ID}}{{IC}}\) và \(\widehat {AID} = \widehat {BIC}\)
\( \Rightarrow \)\(\Delta IAD \backsim \Delta IBC\) (c-g-c)

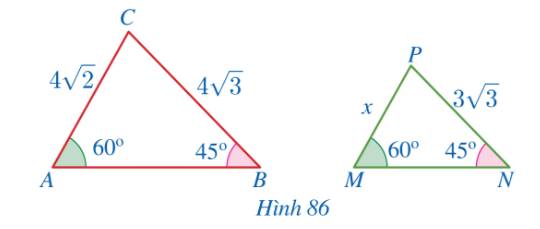
a) Xét tam giác ABC và tam giác MNP có:
\(\begin{array}{l}\widehat A = \widehat M = 60^\circ \\\widehat B = \widehat N = 45^\circ \end{array}\)
\( \Rightarrow \Delta ABC \backsim \Delta MNP\) (g-g)
b) Vì \(\Delta MNP \backsim \Delta ABC\) nên \(\frac{{AC}}{{MP}} = \frac{{BC}}{{NP}}\) (Tỉ số đồng dạng)
\(\begin{array}{l} \Rightarrow \frac{{4\sqrt 2 }}{x} = \frac{{4\sqrt 3 }}{{3\sqrt 3 }}\\ \Rightarrow x = \frac{{4\sqrt 2 .3\sqrt 3 }}{{4\sqrt 3 }} = 3\sqrt 2 \end{array}\)

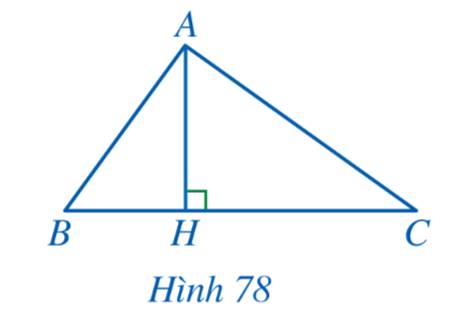
a) Ta có:
\(A{H^2} = BH.CH \Rightarrow AH.AH = BH.CH \Rightarrow \frac{{AH}}{{CH}} = \frac{{BH}}{{AH}}\)
Xét tam giác HAB và tam giác HCA có:
\(\frac{{AH}}{{CH}} = \frac{{BH}}{{AH}}\) và \(\widehat {AHB} = \widehat {CHA} = 90^\circ \)
\( \Rightarrow \Delta HAB \backsim \Delta HCA\) (c-g-c)
b) Vì \(\Delta HAB \backsim \Delta HCA\) nên \(\widehat {HBA} = \widehat {HAC}\)
Xét tam giác AHB vuông tại H có:
\(\begin{array}{l}\widehat {HAB} + \widehat {HBA} = 90^\circ \\ \Rightarrow \widehat {HAB} + \widehat {HAC} = 90^\circ \\ \Rightarrow \widehat {BAC} = 90^\circ \end{array}\)
Vậy tam giác ABC vuông tại A.

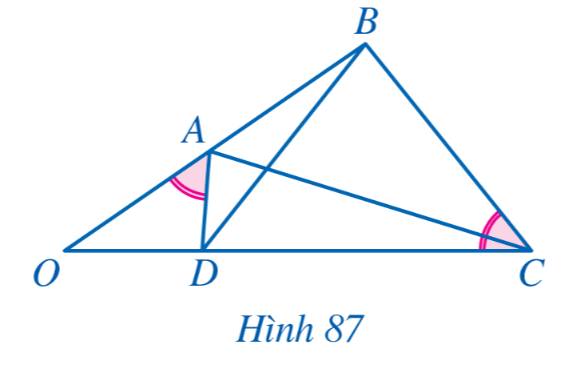
a) Xét tam giác OAD và tam giác OCB có:
\(\widehat {OAD} = \widehat {OCB};\,\,\widehat O\) chung
\( \Rightarrow \Delta OAD \backsim \Delta OCB\) (g-g)
b) Vì \(\Delta OAD \backsim \Delta OCB\) nên ta có \(\frac{{OA}}{{OC}} = \frac{{OD}}{{OB}}\) (Tỉ số đồng dạng)
\( \Rightarrow \frac{{OA}}{{OD}} = \frac{{OC}}{{OB}}\)
c) Xét tam giác OAC và tam giác ODB có:
\(\frac{{OA}}{{OD}} = \frac{{OC}}{{OB}}\) và \(\widehat O\) chung
\( \Rightarrow \Delta OAC \backsim \Delta ODB\) (c-g-c)

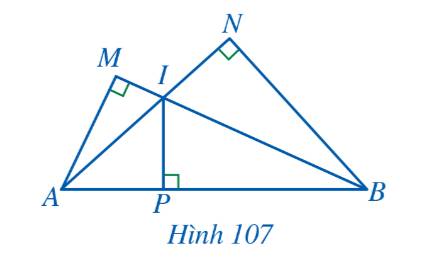
a) Xét tam giác ABN và tam giác AIP có:
\(\widehat {ANB} = \widehat {API} = 90^\circ \) và \(\widehat A\) chung
\( \Rightarrow \)\(\Delta ABN \backsim \Delta AIP\) (g-g)
\( \Rightarrow \frac{{AB}}{{AI}} = \frac{{AN}}{{AP}} \Rightarrow AI.AN = AP.AB\)
b) Xét tam giác AMB và tam giác IPB có:
\(\widehat {AMB} = \widehat {IPB} = 90^\circ \) và \(\widehat B\) chung
\( \Rightarrow \)\(\Delta AMB \backsim \Delta IPB\) (g-g)
\( \Rightarrow \frac{{AB}}{{BI}} = \frac{{BM}}{{BP}} \Rightarrow BI.BM = AP.PB\)
Khi đó:
\(AI.AN + BI.BM = AP.AB + AB.PB = AB\left( {AP + PB} \right) = A{B^2}\)

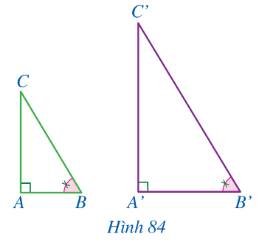
Xét tam giác A’B’C’ và tam giác ABC có:
\(\widehat {A'} = \widehat A,\,\,\widehat {B'} = \widehat B\)
\( \Rightarrow \Delta A'B'C' \backsim \Delta ABC\) (g-g)

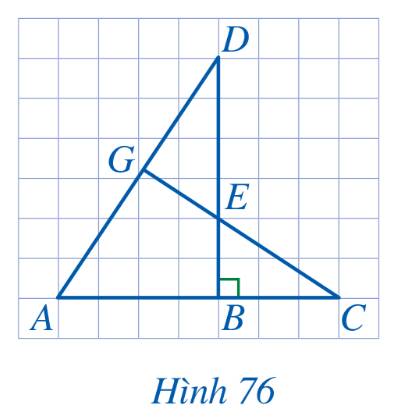
a) Ta có: \(\frac{{AB}}{{EB}} = \frac{4}{2} = 2;\,\,\frac{{BD}}{{BC}} = \frac{6}{3} = 2\)
\( \Rightarrow \frac{{AB}}{{EB}} = \frac{{BD}}{{BC}}\)
Xét tam giác ABD và tam giác EBC có:
\(\frac{{AB}}{{EB}} = \frac{{BD}}{{BC}}\) và \(\widehat {ABD} = \widehat {EBC} = 90^\circ \)
\( \Rightarrow \Delta ABD \backsim \Delta EBC\) (c-g-c).
b) Vì \(\Delta ABD \backsim \Delta EBC\) nên \(\widehat {DAB} = \widehat {CEB}\)
Mà \(\widehat {DEG} = \widehat {CEB}\) (hai góc đối đỉnh) nên \(\widehat {DAB} = \widehat {DEG}\).
c) Vì \(\Delta ABD \backsim \Delta EBC\) nên \(\widehat {ADB} = \widehat {ECB}\) hay \(\widehat {GDE} = \widehat {ECB}\)
Vì tam giác EBC vuông tại B nên ta có:
\(\begin{array}{l}\widehat {ECB} + \widehat {CEB} = 90^\circ \\ \Rightarrow \widehat {GDE} + \widehat {DEG} = 90^\circ \end{array}\)
Mà trong tam giác DEG có:
\(\begin{array}{l}\widehat {GDE} + \widehat {DEG} + \widehat {DGE} = 180^\circ \\ \Rightarrow 90^\circ + \widehat {DGE} = 180^\circ \\ \Rightarrow \widehat {DGE} = 90^\circ \end{array}\)
\( \Rightarrow \)Tam giác DGE vuông tại G.

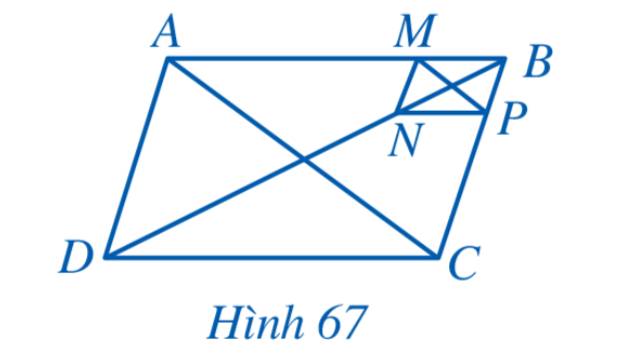
a) Vì ABCD và BMNP là hình bình hành nên \(MN//BP\) và \(AD//BC \Rightarrow MN//AD\)
Xét tam giác ABD có \(AD//MN \Rightarrow \frac{{BM}}{{BA}} = \frac{{BN}}{{BD}}\) (1) (Định lý Thales)
Tương tự ta chứng minh được \(NP//DC \Rightarrow \frac{{BN}}{{BD}} = \frac{{BP}}{{BC}}\)(2)
Từ (1) và (2) ta có \(\frac{{BM}}{{BA}} = \frac{{BP}}{{BC}}\).
b) Ta có \(\frac{{BM}}{{BA}} = \frac{{BP}}{{BC}} \Rightarrow MP//AC\)(Định lý Thales đảo)
\( \Rightarrow \Delta PBM \backsim\Delta CBA\) (c-c-c) (3)
Vì BMNP là hình bình hành nên ta có \(\frac{{PB}}{{MN}} = \frac{{BM}}{{NP}} = \frac{{MP}}{{PM}} = 1\)
\( \Rightarrow \Delta PBM \backsim\Delta MNP\) (c-c-c) (4)
Từ (3) và (4) ta có \(\Delta MNP \backsim\Delta CBA\).

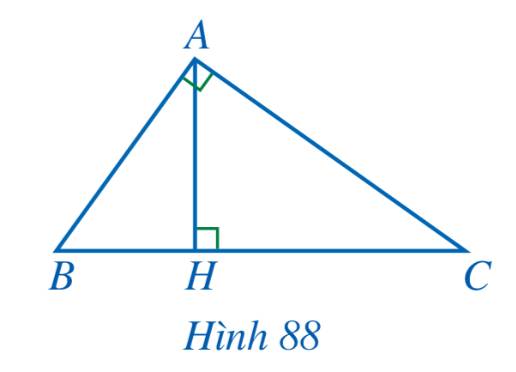
a) Xét tam giác ABC và tam giác HBA có:
\(\widehat {BAC} = \widehat {BHA} = 90^\circ ;\,\,\widehat B\) chung
\( \Rightarrow \Delta ABC \backsim \Delta HBA\) (g-g)
\( \Rightarrow \frac{{AB}}{{HB}} = \frac{{BC}}{{BA}} \Rightarrow A{B^2} = BC.HB\)
b) Xét tam giác ABC và tam giác HAC có:
\(\widehat {BAC} = \widehat {AHC} = 90^\circ ;\,\,\widehat C\) chung
\( \Rightarrow \Delta ABC \backsim \Delta HAC\) (g-g)
\( \Rightarrow \frac{{AC}}{{HC}} = \frac{{BC}}{{AC}} \Rightarrow A{C^2} = BC.CH\)
c) Ta có: \(\Delta ABC \backsim \Delta HBA\) và nên \(\Delta ABH \backsim \Delta CAH\)
\( \Rightarrow \frac{{AH}}{{CH}} = \frac{{BH}}{{AH}} \Rightarrow A{H^2} = BH.CH\)
d) Ta có:
\(A{B^2} = BC.BH \Rightarrow \frac{1}{{A{B^2}}} = \frac{1}{{BC.BH}}\)
\(A{C^2} = BC.CH \Rightarrow \frac{1}{{A{B^2}}} = \frac{1}{{BC.CH}}\)
\(A{H^2} = BH.CH \Rightarrow \frac{1}{{A{H^2}}} = \frac{1}{{BH.CH}}\)
\(\begin{array}{l} \Rightarrow \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{1}{{BC.BH}} + \frac{1}{{BC.CH}}\\ = \frac{1}{{BC}}.\left( {\frac{1}{{BH}} + \frac{1}{{CH}}} \right)\\ = \frac{1}{{BC}}.\frac{{BH + CH}}{{BH.CH}}\\ = \frac{1}{{BC}}.\frac{{BC}}{{BH.CH}}\\ = \frac{1}{{BH.CH}}\\ = \frac{1}{{A{H^2}}}\end{array}\)
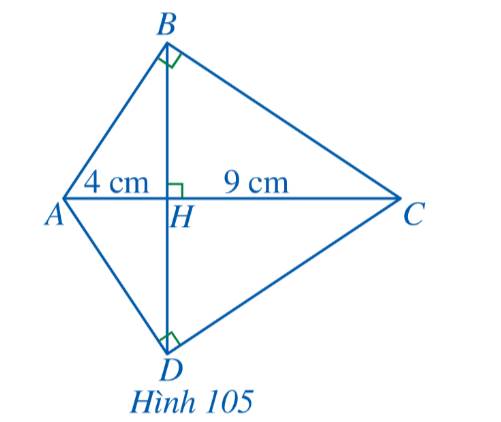
a) Xét tam giác ABC vuông tại B có: \(\widehat {BAC} + \widehat {BCA} = 90^\circ \)
Xét tam giác BHC vuông tại H có:
\(\begin{array}{l}\widehat {HBC} + \widehat {HCB} = 90^\circ \\ \Rightarrow \widehat {HBC} + \widehat {BCA} = 90^\circ \end{array}\)
\( \Rightarrow \widehat {HBC} = \widehat {BAC}\) hay \(\widehat {HBC} = \widehat {BAH}\)
Xét tam giác HAB và tam giác HBC có:
\(\widehat {BAH} = \widehat {CBH}\) và \(\widehat {BHA} = \widehat {CHB} = 90^\circ \)
\( \Rightarrow \Delta HAB \backsim \Delta HBC\)
b) Vì \(\Delta HAB \backsim \Delta HBC\) nên
\(\begin{array}{l}\frac{{HA}}{{HB}} = \frac{{HB}}{{HC}}\\ \Rightarrow H{B^2} = HA.HC\\ \Rightarrow H{B^2} = 4.9 = 36\\ \Rightarrow HB = 6cm\end{array}\)
Ta chứng minh được \(\Delta HAD \backsim \Delta HDC\)
\(\begin{array}{l} \Rightarrow \frac{{HA}}{{HD}} = \frac{{HD}}{{HC}}\\ \Rightarrow H{D^2} = HA.HC\\ \Rightarrow H{D^2} = 4.9 = 36\\ \Rightarrow HD = 6cm\end{array}\)
Vậy \(HB = HD = 6cm\).