
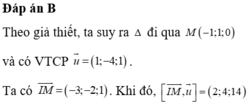
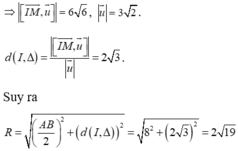
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

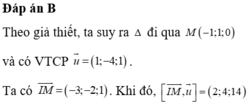
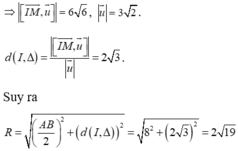

a) Trục Ox là đường thẳng đi qua O(0, 0, 0) và nhận i→=(1,0,0) làm vectơ chỉ phương nên có phương trình tham số là:
* Tương tự, trục Oy có phương trình
Trục Oz có phương trình
b) Đường thẳng đi qua M0 (x0,y0,z0) song song với trục Ox sẽ có vectơ chỉ phương là i→(1,0,0) nên có phương trình tham số là:
tương tự ta có Phương trình của đường thẳng đi qua M0 (x0,y0,z0) và song song với Oy là:
phương trình đường thẳng đi qua M0 (x0,y0,z0) và song song với Oz là
c) Đường thẳng đi qua M(2, 0, -1) và có vectơ chỉ phương u→(-1,3,5) có phương trình tham số là
có phương trình chính tắc là
d) Đường thẳng đi qua N(-2, 1, 2) và có vectơ chỉ phương u→(0,0,-3) có phương trình tham số là
Đường thẳng này không có Phương trình chính tắc.
e) Đường thẳng đi qua N(3, 2, 1) và vuông góc với mặt phẳng: 2x- 5y + 4= 0 nên nó nhận vectơ pháp tuyến của mặt phẳng này làn→(2,-5,0) là vectơ chỉ phương, nên ta có phương trình tham số là
Đường thẳng này không có Phương trình chính tắc.
f) Đường thẳng đi qau P(2, 3, -1) và Q(1, 2, 4) sẽ nhận PQ→(-1,-1,5) là vectơ chỉ phương, nên có phương trình tham số là
và có phương tình chính tắc là

Chọn A
Gọi ![]() là một vec tơ pháp tuyến của mặt phẳng (P).
là một vec tơ pháp tuyến của mặt phẳng (P).
Theo đề bài ta có mặt phẳng (P) vuông góc với mặt phẳng (α): x-y+z-4=0 nên ta có phương trình a-b+c=0 ó b=a+c ![]()
Phương trình mặt phẳng (P) đi qua A(0;1;2) và có véc tơ pháp tuyến là ax+ (a+c) (y-1)+c (z-2) =0
Khoảng cách từ tâm I (3;1;2) đến mặt phẳng (P) là 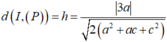
Gọi r là bán kính của đường tròn giao tuyến giữa mặt cầu (S) và mặt phẳng (P) ta có r²=16-h² ; r nhỏ nhất khi h lớn nhất.
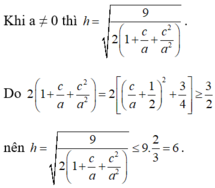
Dấu “=” xảy ra khi a = -2c. => một véc tơ pháp tuyến là ![]() => phương trình mặt phẳng (P) là 2x+y-z+1=0.
=> phương trình mặt phẳng (P) là 2x+y-z+1=0.
Vậy tọa độ giao điểm M của (P) và trục x'Ox là: 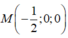

Chọn C
* Ta có: ![]() trong đó a;b;c không đồng thời bằng 0. Mặt cầu (S) có tâm I (1;2;3) và bán kính R=5.
trong đó a;b;c không đồng thời bằng 0. Mặt cầu (S) có tâm I (1;2;3) và bán kính R=5.
Do mặt phẳng (P) chứa đường thẳng AB nên ta có:
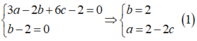
* Bán kính đường tròn giao tuyến là ![]() trong đó
trong đó
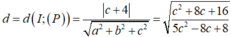
Để bán kính đường tròn nhỏ nhất điều kiện là d lớn nhất 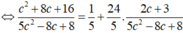 lớn nhất
lớn nhất 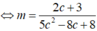 lớn nhất.
lớn nhất.
Coi hàm số ![]() là một phương trình ẩn c ta được
là một phương trình ẩn c ta được
5mc²-2 (4m+1)c+ (8m-3)=0,
phương trình có nghiệm c 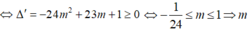 lớn nhất
lớn nhất
<=> c = 1 => a = 0 => M = 2a + b – c = 1

19.
Phương trình mặt phẳng theo đoạn chắn:
\(\frac{x}{3}+\frac{y}{-4}+\frac{z}{-2}=1\)
\(\Leftrightarrow4x-3y-6z-12=0\)
20.
Phương trình mặt phẳng (ABC) theo đoạn chắn:
\(\frac{x}{1}+\frac{y}{2}+\frac{z}{3}=1\)
\(\Leftrightarrow6x+3y+2z-6=0\)
Chẳng đáp án nào đúng cả, chắc bạn ghi nhầm đáp án C số 1 thành số 0 :)
15.
\(2\left(x-2\right)-5\left(y+3\right)+1\left(z+2\right)=0\)
16.
\(\overrightarrow{n_1}=\left(1;1;-1\right)\) ; \(\overrightarrow{n_2}=\left(1;-1;1\right)\)
\(\left[\overrightarrow{n_1};\overrightarrow{n_2}\right]=\left(0;-2;-2\right)=-2\left(0;1;1\right)\)
Phương trình (P):
\(1\left(y-1\right)+1\left(z-1\right)=0\Leftrightarrow y+z-2=0\)
17.
\(\overrightarrow{n_P}=\left(1;-1;1\right)\) ; \(\overrightarrow{n_Q}=\left(3;2;-12\right)\)
\(\left[\overrightarrow{n_P};\overrightarrow{n_Q}\right]=\left(10;15;5\right)=5\left(2;3;1\right)\)
Phương trình mặt phẳng (R):
\(2x+3y+z=0\)
18.
\(\overrightarrow{MN}=\left(0;-2;3\right);\overrightarrow{MP}=\left(-2;1;3\right)\)
\(\left[\overrightarrow{MN};\overrightarrow{MP}\right]=\left(-9;-6;-4\right)=-1\left(9;6;4\right)\)
Phương trình:
\(9\left(x-2\right)+6\left(y-2\right)+4z=0\)
\(\Leftrightarrow9x+6y+4z-30=0\)