Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D M N O F E
a)
Tứ giác BMDN có BN=DM (=1/2AD=1/2BC) VÀ BN//DM (AD//BC) nên BMDN là hình bình hành. => BM//DN
Tam giác ADF có:
M là trung điểm của AD
ME//DF ( BM//DN )
Suy ra E là trung điểm của AF hay AE=EF (1)
Tam giác BCE có:
N là trung điểm của BC
NF//DE ( BM//DN )
Suy ra F là trung điểm của CE hay EF=FC (2)
Từ (1) và (2) suy ra AE=EF=FC
b)
Xét \(\Delta AME\)và \(\Delta CNF\)CÓ
AM=CN ( =1/2AD = 1/2BC )
AE=CF (Theo câu a)
\(\widehat{MAE}=\widehat{NCF}\)(Vì AD//BC)
Suy ra \(\Delta AME=\Delta CNF\left(c.g.c\right)\)
\(\Rightarrow ME=NF\)( 2 cạnh tương ứng)
Mà ME//NF ( Vì BM//DN ) nên tứ giác MENF là hình bình bình hành
Các bạn nhớ k ủng hộ mik nha! Thanks!

ta có MD//BN ( AB//CD)
MD=BN(AD=BC,MD=AM,BN=NC)
=> BMDN là hình bình hành
a: Xét tứ giác BMDN có
BN//DM
BN=DM
Do đó: BMDN là hình bình hành
=>BM//DN
Xét ΔADF có
M là trung điểm của AD
ME//DF
Do đó: E là trung điểm của AF
=>AE=EF
Xét ΔCEB có
N là trung điểm của CB
NF//EB
DO đó: F là trung điểm của CE
=>AE=EF=FC
b: AE+EO=AO
CF+FO=CO
mà AO=CO; AE=CF
nên EO=FO
=>O là trung điểm của EF
BMDN là hình bình hành
nên BD cắt MN tại trung điểm của mỗi đường
=>O là trung điểm của MN
Xét tứ giác MENF có
O làtrung điểm chung của MN và FE
nên MENF là hình bình hành

a,Hình bình hành ABCD có AB=CD
⇒12AB=AM=12CD=CN⇒12AB=AM=12CD=CN
Mặt khác, M,N lần lượt là trung điểm của AB và CD
Do đó, AM//CN
Tứ giác AMCN có cặp cạnh đối vừa song song vừa bằng nhau nên là hình bình hành (đpcm)
b, Tứ giác AMCN là hình bình hành
⇒⇒M1ˆ=N1ˆM1^=N1^ (Hai góc đối của hình bình hành AMCN)
⇒⇒M2ˆ=N2ˆM2^=N2^ (Do M1ˆM1^ và M2ˆM2^ là hai góc kề bù; N1ˆN1^ và N2ˆN2^ là hai góc kề bù)
Mặt khác, ABCD là hình bình hành nên AB//CD ⇒⇒B1ˆ=D1ˆB1^=D1^
ΔEDNΔEDN và ΔKBMΔKBM có:
M2ˆ=N2ˆM2^=N2^
DN=BMDN=BM
B1ˆ=D1ˆB1^=D1^
⇒ΔEDN=ΔKBM(g.c.g)⇒ΔEDN=ΔKBM(g.c.g)
⇒ED=KB⇒ED=KB (đpcm)
c, Gọi O là giao điểm của AC và BD.
ABCD là hình bình hành
⇒OA=OC⇒OA=OC
ΔCABΔCAB có:
MA=MBMA=MB
OA=OCOA=OC
MC cắt OB tại K
⇒⇒ K là trọng tâm của ΔCABΔCAB
Mặt khác, I là trung điểm của BC
⇒⇒ IA,OB,MC đồng quy tại K
Hay AK đi qua trung điểm I của BC (đpcm)

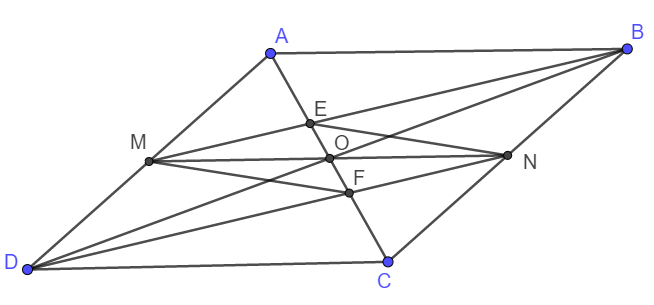
a) Do ABCD là hình bình hành nên AD song song và bằng BC.
Lại có M, N là trung điểm AD, BC nên DM song song và bằng BN. Suy ra DMBN là hình bình hành, hay MB//DN.
Xét tam giác ADF, có:
M là trung điểm AC
ME//DF
\(\Rightarrow\) ME là đường trung bình tam giác ADF.
Vậy AE = EF.
Hoàn toàn tương tự : EF = FC.
Vậy nên AE = EF = FC.
b) DMBN là hình bình hành nên hai đường chéo DB và MN cắt nhau tại trung điểm mỗi đường.
Vậy thì O là trung điểm MN.
Lại có: AO = OC; AE = FC nên AO - AE = OC - FC hay EO = OF.
Xét tứ giác MENF có O là trung điểm hai đường chéo EF và MN nên MENF là hình bình hành.
c)
+) Để hình bình hành MENF là hình chữ nhật thì hai đường chéo MN và EF bằng nhau.
Lại có MN = AB, EF = \(\frac{AC}{3}\). Vậy hình bình hành ABCD phải có đường chéo AC = 2AB thì MENF là hình chữ nhật.
+) Để hình bình hành MENF là hình thoi thì hai đường chéo MN và EF phải vuông góc.
Vậy thì \(EF\perp MN\Rightarrow AC\perp AB\)
Vậy hình bình hành ABCD phải có đường chéo AC vuông góc với cạnh AB thì MENF là hình thoi.
+) Để hình bình hành MENF là hình vuông thì nó vừa là hình chữ nhật, vừa là hình thoi.
Vậy thì hình bình hành ABCD có đường chéo AC vuông góc với AB và AC = 2AB.

a: Xét tứ giác BMDN có
DM//BN
DM=BN
Do đó: BMDN là hình bình hành
a: Xét tứ giác BMDN có
BN//DM
BN=DM
Do đó: BMDN là hình bình hành
=>BM//DN
Xét ΔADF có
M là trung điểm của AD
ME//DF
Do đó: E là trung điểm của AF
=>AE=EF
Xét ΔCEB có
N là trung điểm của CB
NF//EB
DO đó: F là trung điểm của CE
=>AE=EF=FC
b: AE+EO=AO
CF+FO=CO
mà AO=CO; AE=CF
nên EO=FO
=>O là trung điểm của EF
BMDN là hình bình hành
nên BD cắt MN tại trung điểm của mỗi đường
=>O là trung điểm của MN
Xét tứ giác MENF có
O làtrung điểm chung của MN và FE
nên MENF là hình bình hành