Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1)
a) Xét phương trình hoành độ giao điểm: \(2x+3+m=3x+5-m\)
\(\Leftrightarrow x=3+m+m-5\Leftrightarrow x=2m-2\)
Để giao điểm của hai đường thẳng trên nằm trên trục tung thì \(2m-2=0\Leftrightarrow m=1\)
b) Do (d) // (d') nên (d) có phương trình \(y=-\frac{1}{2}x+b\)
Do (d) cắt trục hoành tại điểm có hoành độ x = 10 nên điểm (10;0) thuộc đường thẳng (d0.
Vậy thì \(0=-\frac{1}{2}.10+b\Leftrightarrow b=5\)
Vậy phương trình đường thẳng (d) là \(y=-\frac{1}{2}x+5\)
Bài 2)
a) Để (d1)//(d2) thì \(4m=3m+1\Leftrightarrow m=1\)
b) Để (d1)//(d2) thì \(4m\ne3m+1\Leftrightarrow m\ne1\)
Khi m = 2, ta có phương trình hoành độ giao điểm là:
\(8x-7=7x-7\Leftrightarrow x=0\)
Với \(x=0,y=-7\)
Vậy tọa độ giao điểm của (d1) và (d2) là (0; -7)

b) Phương trình hoành độ giao điểm của (P) và (d):
x² = mx - m + 1
⇔ x² - mx + m - 1 = 0
∆ = m² - 4.1.(m - 1)
= m² - 4m + 4
= (m - 2)² ≥ 0 với mọi m ∈ R
⇒ Phương trình luôn có hai nghiệm
Theo Viét ta có:
x₁ + x₂ = m (1)
x₁x₂ = m - 1 (2)
Lại có x₁ + 3x₂ = 7 (3)
Từ (1) ⇒ x₁ = m - x₂ (4)
Thay x₁ = m - x₂ vào (3) ta được:
m - x₂ + 3x₂ = 7
2x₂ = 7 - m
x₂ = (7 - m)/2
Thay x₂ = (7 - m)/2 vào (4) ta được:
x₁ = m - (7 - m)/2
= (2m - 7 + m)/2
= (3m - 7)/2
Thay x₁ = (3m - 7)/2 và x₂ = (7 - m)/2 vào (2) ta được:
[(3m - 7)/2] . [(7 - m)/2] = m - 1
⇔ 21m - 3m² - 49 + 7m = 4m - 4
⇔ 3m² - 28m + 49 + 4m - 4 = 0
⇔ 3m² - 24m + 45 = 0
∆' = 144 - 3.45 = 9 > 0
Phương trình có hai nghiệm phân biệt:
m₁ = (12 + 3)/3 = 5
m₂ = (12 - 3)/3 = 3
Vậy m = 3; m = 5 thì (P) và (d) cắt nhau tại hai điểm có hoành độ thỏa mãn x₁ + 3x₂ = 7

Do đường thẳng qua M nên: \(4a+b=3\Rightarrow b=3-4a\)
b dương \(\Rightarrow3-4a>0\Rightarrow a< \dfrac{3}{4}\) (1)
Pt đường thẳng: \(y=ax-4a+3\)
Giao điểm với trục hoành:
\(ax-4a+3=0\Rightarrow x=\dfrac{4a-3}{a}=4-\dfrac{3}{a}\)
Do hoành độ là số nguyên \(\Rightarrow3-\dfrac{3}{a}\in Z\)
\(\Leftrightarrow\dfrac{3}{a}\in Z\) \(\Rightarrow a=\left\{-3;-1;1;3\right\}\)
Kết hợp điều kiện (1) \(\Rightarrow a=\left\{-3;-1\right\}\)
\(\Rightarrow b=\left\{15;7\right\}\)
Vậy \(\left(a;b\right)=\left(-3;15\right);\left(-1;7\right)\)

b) (d) cắt (P) tại 2 điểm A, B phân biệt nằm về 2 phía của trục tung khi và chỉ khi
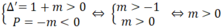
Khi đó 2 nghiệm của phương trình là:
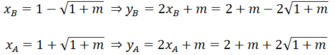
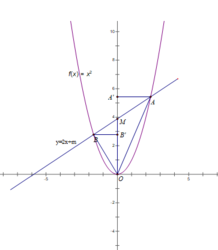
Kẻ BB' ⊥ OM ; AA' ⊥ OM
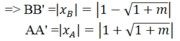
Ta có:
S A O M = 1/2 AA'.OM ; S B O M = 1/2 BB'.OM
Theo bài ra:
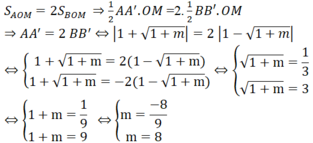
Do m > 0 nên m = 8
Vậy với m = 8 thì thỏa mãn điều kiện đề bài.

Đề thi tuyển sinh THPT Hoàng Văn Thụ, Hòa Bình, 2013-2014
Giải:
PT hoành độ giao điểm là (m+1)m=x2
<=> x2-(m+1)x+m=0
\(\Delta=\left(m+1\right)^2-4m=m^2-2m+1=\left(m-1\right)^2,m\ne1\)
\(\sqrt{\Delta}=m-1\)
\(x_1=\frac{m+1+m-1}{1}=2m\)
\(\Rightarrow y_1=\left(2m\right)^2-\left(m+1\right)2m+m=4m^2-2m^2-2m+m=2m^2-m\)
\(x_2=\frac{m+1-m+1}{1}=2\)
\(\Rightarrow y_2=4-\left(m+1\right)\cdot2+m=4-2m-2+m=2-m\)
=> A(2m;2m2-m)





