Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ Ta có: -3 < 1 nên 4 + (-3) < 4 + 1 hay 4 + (-3) < 5
→ Khẳng định ( 1 ) đúng.
+ Ta có: 6 ≤ 7 ⇒ 6 + (-2) ≤ 7 + (-2)
→ Khẳng định ( 2 ) đúng.
+ Ta có: 24 < 25 ⇒ 24 + ( - 5 ) < 25 + ( - 5 )
→ Khẳng định ( 3 ) sai.
Chọn đáp án C.

a) Thay x=-1 vào 2 vế của phương trình trên , ta được :
\(VT=\left(-1\right)^3+3.\left(-1\right)=-4\left(1\right)\)
\(VP=2.\left(-1\right)^2-3.\left(-1\right)+1=6\left(2\right)\)
Từ (1) và (2) \(\Rightarrow VT\ne VP\)
* Vậy x = -1 không phải là nghiệm của phương trình trên .
b) Thay z=3 vào 2 vế của phương trình trên , ta được :
\(VT=\left(3-2\right)\left(3^2+1\right)=10\left(1\right)\)
\(VP=2.3+5=11\left(2\right)\)
Từ (1) và (2) \(\Rightarrow VT\ne VP\)
* Vậy z=3 không phải là nghiệm của phương trình trên .

1. Trong các phương trình sau, phương trình bậc nhất 1 ẩn là
A. 2/x - 7=0; B. |7x+5)-1=0; C. 8x-9=0
2. điều kiện xác định của phương trình
\(\frac{4}{2x-3}=\frac{7}{3x-5}\)là
A. x khác 3/2. B. x khác5/3; C. x khác 3/2 hoặc 5/3; D. x khác 3/2 và 5/3
1.Pt bậc nhất 1 ẩn:\(8x-9=0\)
2.ĐKXĐ:\(x\ne\frac{3}{2};x\ne\frac{5}{3}\)

Ta có: VT = (-2) + 3 = 1
VP = 2
=> VT < VP nên khẳng định (-2) + 3 ≥ 2 là sai.
b) Ta có: VT = -6
VP = 2.(-3) = -6
=> VT = VP nên khẳng định -6 ≤ 2.(-3) là đúng.
c) Ta có: VT = 4 + (-8) = -4
VP = 15 + (-8) = 7
=> VP > VT nên khẳng định 4 + (-8) < 15 + (-8) là đúng.
d) Vì \(x^2\) ≥ 0 với mọi x ∈ R
=> \(x^2\) + 1 ≥ 0 + 1
=> \(x^2\) + 1 ≥ 1
Vậy khẳng định \(x^2\)+ 1 ≥ 1 là đúng.
(Kí hiệu: VP = vế phải; VT = vế trái)
a) Ta có: VT = (-2) + 3 = 1
VP = 2
=> VT < VP nên khẳng định (-2) + 3 \(\ge\) 2 là sai.
b) Ta có: VT = -6
VP = 2.(-3) = -6
=> VT = VP nên khẳng định -6 \(\le\) 2.(-3) là đúng.
c) Ta có: VT = 4 + (-8) = -4
VP = 15 + (-8) = 7
=> VP > VT nên khẳng định 4 + (-8) < 15 + (-8) là đúng.
d) Vì x2 \(\ge\)0 với mọi x ∈ R
=> x2 + 1 \(\ge\) 0 + 1
=> x2 + 1 \(\ge\) 1
Vậy khẳng định x2 + 1 \(\ge\) 1 là đúng.

a) (-6).5 < (-5).5
Vì -6 < -5 và 5 > 0
=> (-6).5 < (-5).5
Vậy khẳng định (-6).5 < (-5).5 là đúng
b) -6 < -5 và -3 < 0
=> (-6).(-3) > (-5).(-3)
Vậy khẳng định (-6).(-3) < (-5).(-3) là sai.
c) -2003 ≤ 2004 và -2005 < 0
=> (-2003).(-2005) ≥ (-2005).2004
Vậy khẳng định (-2003).(-2005) ≤ (-2005).2004 là sai.
d) x2 ≥ 0 và -3 < 0
=> -3x2 ≤ 0
Vậy khẳng định -3x2 ≤ 0 là đúng

\(\frac{4}{2x+3}-\frac{7}{3x-5}=0\left(đkxđ:x\ne-\frac{3}{2};\frac{5}{3}\right)\)
\(< =>\frac{4\left(3x-5\right)}{\left(2x+3\right)\left(3x-5\right)}-\frac{7\left(2x+3\right)}{\left(2x+3\right)\left(3x-5\right)}=0\)
\(< =>12x-20-14x-21=0\)
\(< =>2x+41=0< =>x=-\frac{41}{2}\left(tm\right)\)
\(\frac{4}{2x-3}+\frac{4x}{4x^2-9}=\frac{1}{2x+3}\left(đk:x\ne-\frac{3}{2};\frac{3}{2}\right)\)
\(< =>\frac{4\left(2x+3\right)}{\left(2x-3\right)\left(2x+3\right)}+\frac{4x}{\left(2x-3\right)\left(2x+3\right)}-\frac{2x-3}{\left(2x+3\right)\left(2x-3\right)}=0\)
\(< =>8x+12+4x-2x+3=0\)
\(< =>10x=15< =>x=\frac{15}{10}=\frac{3}{2}\left(ktm\right)\)

a, - Để biểu thức trên được xác định thì : \(x^2+x+1\ne0\)
Mà \(x^2+x+1=\left(x+\frac{1}{2}\right)^2+\frac{3}{4}>0\)
Vậy biểu thức luôn được xác định với mọi x .
b, - Để biểu thức trên được xác định thì : \(4x^2+2x+3\ne0\)
Mà \(4x^2+2x+3=\) \(x^2+\frac{x}{2}+\frac{3}{4}=\left(x+\frac{1}{4}\right)^2+\frac{11}{16}>0\)
Vậy biểu thức luôn được xác định với mọi x .
d, - Để biểu thức trên có nghĩa thì : \(3t^2-t+1\ne0\)
Mà \(3t^2-t+1=3\left(t^2-\frac{t}{3}+\frac{1}{3}\right)=3\left(\left(t-\frac{1}{6}\right)^2+\frac{11}{36}\right)>0\)
Vậy biểu thức luôn được xác định với mọi x .

\(\left(x+1\right)\left(x^2-x-x^2+x-1\right)=-\left(x+1\right)\)
\(\left(2a^2+1\right)^2-4a^2-\left(2a^2+1\right)^2=-4a^2\)
\(\left(a^2+b^2+c^2+a^2-b^2-c^2\right)\left(a^2+b^2+c^2-a^2+b^2+c^2\right)=2a^2\left(2b^2+2c^2\right)=4a^2b^2+4a^2c^2\)
\(\left(a-5\right)^2\left(a+5\right)^2=\left(a^2-25\right)^2\)
\(\left(3a^3+1\right)^2-9a^2-\left(3a^3+1\right)^2=-9a^2\)
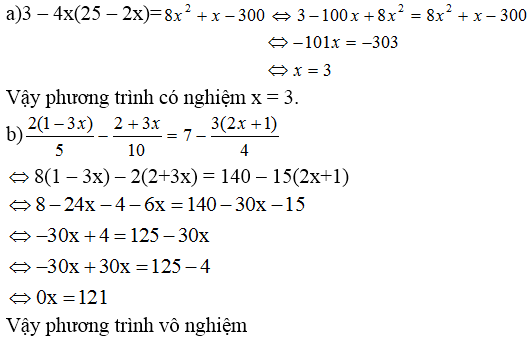

+ Ta có: -3 < 1 nên 4 + (-3) < 4 + 1 hay 4 + (-3) < 5
Khẳng định ( 1 ) đúng.
+ Ta có: 6 < 7 nên 6 + (-2) < 7 + (-2)
Khẳng định ( 2 ) đúng.
+ Ta có: 24 < 25 ⇒ 24 + ( - 5 ) < 25 + ( - 5 )
→ Khẳng định ( 3 ) sai.
Chọn đáp án C.