Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải:
Oxyt
a. Ta có:\(\widehat{xOt}>\widehat{xOy}\left(60^o< 120^o\right)\)
\(\Leftrightarrow\)Tia \(Oy\)nằm giữa hai tia \(Ox,Ot\)
b. Vì tia \(Oy\)nằm giữa hai tia \(Ox,Ot\)nên:
\(\Leftrightarrow\widehat{xOy}+\widehat{yOt}=\widehat{xOt}\)
\(\Leftrightarrow60^o+\widehat{yOt}=120^o\)
\(\Leftrightarrow\widehat{yOt}=\widehat{xOt}-\widehat{xOy}\)
\(\Leftrightarrow\widehat{yOt}=120^o-60^o\)
\(\Leftrightarrow\widehat{yOt}=60^o\)
Vậy: số đo \(\widehat{yOt}=60^o\)
c. Ta có:
\(\widehat{xOy}=60^o\)
\(\widehat{yOt}=60^o\)
\(\Leftrightarrow\widehat{xOy}=\widehat{yOt}=60^o\)
Vì tia \(Oy\)nằm giữa \(Ox,Ot\)và \(\widehat{xOy}=\widehat{yOt}\)nên \(Oy\)là tia phân giác của \(\widehat{xOt}\)

`Answer:`
a. Theo đề ra: \(\hept{\begin{cases}\widehat{xOy}=60^o\\\widehat{xOt}=120^o\end{cases}}\Rightarrow\widehat{xOy}< \widehat{xOt}\Rightarrow\) Tia `Oy` nằm giữa hai tia `Ox` và `Ot`
b. Ta có: `\hat{xOy}+\hat{yOt}=\hat{xOt}`
`=>60^o+\hat{yOt}=120^o`
`=>\hat{yOt}=60^o`
c. Theo phần a. Tia `Oy` nằm giữa tia `Ox` và `Ot(1)`
Mà `\hat{xOy}=\hat{yOt}=60^o(2)`
Từ `(1)(2)=>` Tia `Oy` là tia phân giác của `\hat{xOt}`

Giải thích các bước giải:
a. Vì trên cùng một nửa mặt phẳng bờ chứa tia Ox, vẽ hai tia Oy và Ot sao cho ∠ xOy=60° và ∠ xOt= 120°
⇒Oy nằm giữa Ot và Ox
b. Vì Oy nằm giữa Ot và Ox:
∠xOy+ ∠yOt=∠xOt∠xOy+ ∠yOt=∠xOt
hay 60°+∠yOt=120°60°+∠yOt=120°
⇒∠yOt=60°⇒∠yOt=60°
c. Vì Oy nằm giữa Ox và Ot
Mà ∠yOt=∠xOy=60°∠yOt=∠xOy=60°
⇒ Oy là tia phân giác của ∠xOt (đpcm)

a)Trên cùng 1 nửa mặt phẳng bờ chứa tia Ox có xOy=30 độ
xOt=70 độ
\(\Rightarrow\)xOy<xOt
nên tia Oy nằm giữa 2 tia Ox và Oy
b)Ta có xOy+yOt=xOt
30 độ+yOt=70 độ
yOt=40 độ
Ta có yOt=40 độ
xOy=30 độ
suy ra yOt>xOy
Vậy tia Oy ko phải là tia phân giác của góc xOt

Giải: Trên cùng một nửa mặt phẳng bờ chứa tia Ox có xOt =65 độ, xOy = 130 độ mà 65 độ < 130 độ
=> Tia Ot nằm giữa 2 tia Ox và Oy (1)
=> yOt+tOx = yOx
Thay số : yOt + 65 độ = 130 độ
yOt =130 độ - 65 độ
yOt=65 độ
=> yOt = tOx (=65độ) (2)
từ (1) và (2) tia Ot là tia phân giác của góc xOy

a) Trên cùng một nửa mặt phẳng bờ chứa tia Ox, ta có: \(\widehat{xOt}< \widehat{xOy}\left(60^0< 120^0\right)\)
nên tia Ot nằm giữa hai tia Ox và Oy
b) Ta có: tia Ot nằm giữa hai tia Ox và Oy(cmt)
nên \(\widehat{xOt}+\widehat{yOt}=\widehat{xOy}\)
\(\Leftrightarrow\widehat{yOt}+60^0=120^0\)
hay \(\widehat{yOt}=60^0\)
Ta có: \(\widehat{xOt}=60^0\)(gt)
mà \(\widehat{yOt}=60^0\)(cmt)
nên \(\widehat{xOt}=\widehat{yOt}\)
c) Ta có: tia Ot nằm giữa hai tia Ox và Oy(cmt)
mà \(\widehat{xOt}=\widehat{yOt}\)(cmt)
nên Ot là tia phân giác của \(\widehat{xOy}\)
d) Ta có: Om là tia phân giác của \(\widehat{xOt}\)
nên \(\widehat{xOm}=\dfrac{60^0}{2}=30^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia Ox, ta có: \(\widehat{xOm}< \widehat{xOy}\left(30^0< 120^0\right)\)
nên tia Om nằm giữa hai tia Ox và Oy
\(\Leftrightarrow\widehat{xOm}+\widehat{mOy}=\widehat{xOy}\)
\(\Leftrightarrow\widehat{mOy}+30^0=120^0\)
hay \(\widehat{mOy}=90^0\)
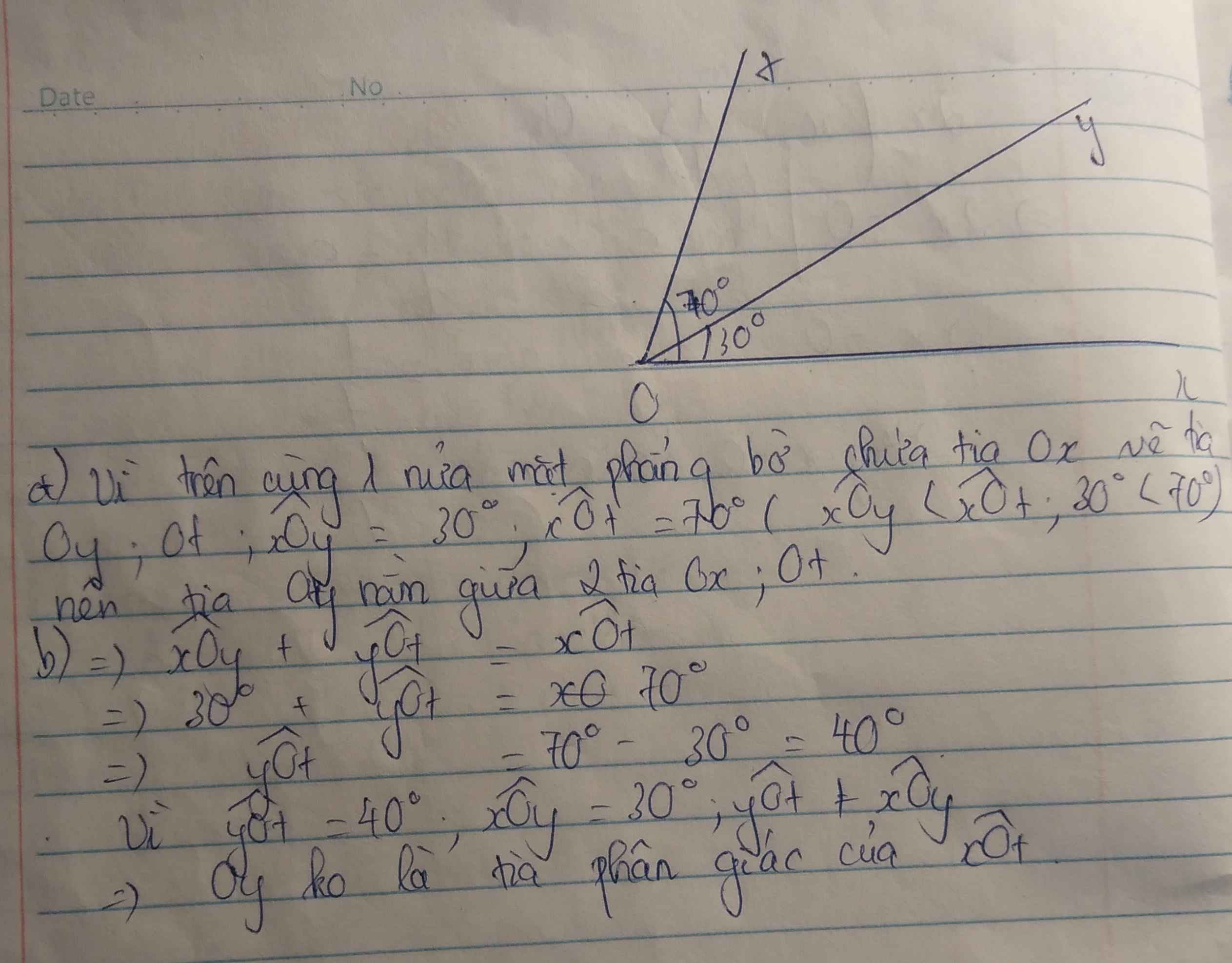
a) Trên cùng 1 nửa mặt phẳng bờ là tia Ox có góc \(\widehat{xOt}\)= 35 độ , góc \(\widehat{xOy}\) = 70 độ => \(\widehat{xOt}\) < \(\widehat{xOy}\) ( vì 35 độ < 70 độ )
=> Tia Ot nằm giữa 2 tia Ox và Oy.
b) Ta có: Tia Ot nằm giữa 2 tia Ox và Oy.
=> góc \(\widehat{xOt}\) + góc \(\widehat{xOy}\) = góc \(\widehat{xOy}\)
=> 35 độ + góc \(\widehat{tOy}\) = 70 độ => góc \(\widehat{tOy}\) = 70 độ - 35 độ = 35 độ
c) Vì góc \(\widehat{xOt}\) = 35 độ, góc \(\widehat{tOy}\) =35 độ nên góc \(\widehat{xOt}\) = góc \(\widehat{tOy}\) (1)
Ta có: Tia Ot nằm giữa 2 tia Ox và Oy => góc\(\widehat{xOt}\) + góc \(\widehat{tOy}\) = góc \(\widehat{xOy}\) (2)
Từ (1) và (2) => Ot là tia phân giác của góc \(\widehat{xOy}\) .