Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì ABCD là hình bình hành nên ta có: \(\overrightarrow {AD} = \overrightarrow {BC} \)\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \) (đpcm)

Từ giả thiết ta có:
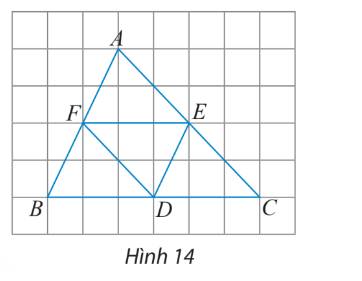
\(AF = FB = ED\); \(AE = EC = FD\); \(BD = DC = EF\)
Từ đó dựa vào hình ta có:
a) Các vectơ bằng vectơ \(\overrightarrow {EF} \)là \(\overrightarrow {DB} \) và \(\overrightarrow {CD} \)
b) Các vectơ đối vectơ \(\overrightarrow {EC} \) là \(\overrightarrow {EA} \) và \(\overrightarrow {DF} \)

Có 7 trận: Tứ kết 1, Tứ kết 2, Tứ kết 3, Tứ kết 4, Bán kết 1, Bán kết 2, Chung kết.

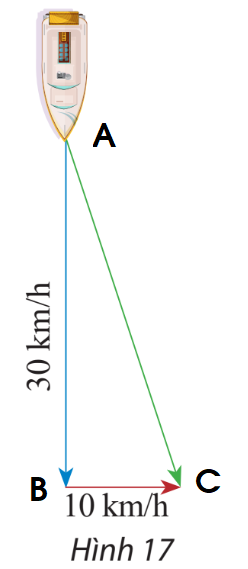
Gọi vecto vận tốc của tàu là \(\overrightarrow {AB} \), vecto vận tốc của dòng nước là vecto \(\overrightarrow {BC} \)
Gọi vecto vận tốc của tàu là \(\overrightarrow {AB} \), vecto vận tốc của dòng nước là vecto \(\overrightarrow {BC} \)
Ta có vecto tổng là \(\overrightarrow F = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Độ dài vecto tổng là \(\left| {\overrightarrow F } \right| = \left| {\overrightarrow {AC} } \right| = AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{30}^2} + {{10}^2}} = 10\sqrt {10} \)(km/h)
Vậy độ dài vecto tổng là \(10\sqrt {10} \)(km/h).
Ta có vecto tổng là \(\overrightarrow F = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Độ dài vecto tổng là \(\left| {\overrightarrow F } \right| = \left| {\overrightarrow {AC} } \right| = AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{30}^2} + {{10}^2}} = 10\sqrt {10} \)(km/h)
Vậy độ dài vecto tổng là \(10\sqrt {10} \)(km/h).

85 km=8500000cm
Tỉ lệ trên bản đồ là:
17:8500000=2/1000000=1/500000
Khoảng cách thực tế giữa 2 điểm A và B là:
12:1/500000=6000000(cm)=60km
ĐS:60 km
Gọi x là khoảng cách giửa A và B trên thực tế
Với khoảng cách giữa hai thành phố = 85 ----------> khoảng cách trên bản đồ là 17
=>khoảng cách giữa A và B = x ----------> khoảng cách trên bản đồ là 12
Ta được tỷ số:
\(\frac{85}{x}=\frac{17}{12}\) => x = \(x=85.12:17=60\)
Vậy x = 60 => khoảng cách của A và B trên thực tế là 60km

\(A=\left(m-2;6\right),B=\left(-2;2m+2\right).\)
Để \(A,B\ne\varnothing\)
\(\Rightarrow\orbr{\begin{cases}m-2\ge-2\\2m+2>6\end{cases}}\Rightarrow\orbr{\begin{cases}m\ge0\\m>2\end{cases}}\)
Kết hợp ĐK \(2< m< 8\)
\(\Rightarrow m\in\left(2;8\right)\)

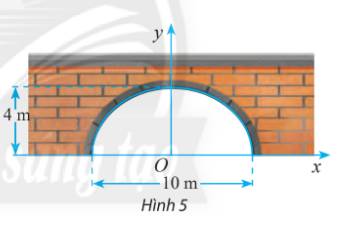
Chiều cao là 4 m tương ứng với \(b = 4\)
Chiều rộng bằng 10 m nên \(2a = 10 \Rightarrow a = 5\)
Vậy phương trình chính tắc của elip có dạng \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{16} = 1\)

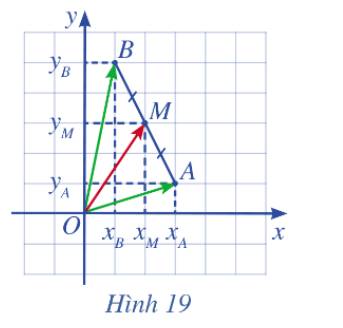
a) Ta có vectơ \(\overrightarrow {OM} \) biểu diễn theo hai vectơ \(\overrightarrow {OA} \) và \(\overrightarrow {OB} \) là: \(\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right)\)
b) Do tọa độ hai điểm A và B là: \(A\left( {{x_A},{y_A}} \right),B\left( {{x_B},{y_B}} \right)\) nên ta có:\(\overrightarrow {OA} = \left( {{x_A},{y_A}} \right),\overrightarrow {OB} = \left( {{x_B},{y_B}} \right)\)
Vậy \(\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right) = \frac{1}{2}\left( {{x_A} + {x_B};{y_A} + {y_B}} \right) = \left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\)
Tọa độ điểm M chính là tọa độ của vectơ nên tọa độ M là \(M\left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\)

Gọi E, F lần lượt là trung điểm của AM, MB; G, H lần lượt là trung điểm của DN, NC.
Ta có P,Q lần lượt là trung điểm của EG, FH. Khi đó

Đáp án C
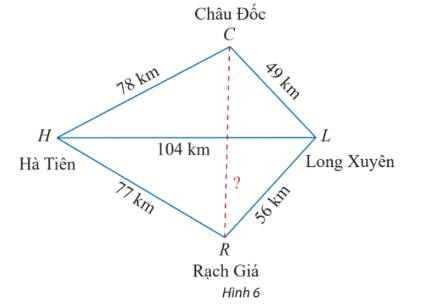



Bước 1: Áp dụng hệ quả của định lí cosin trong tam giác HCL, ta có:
\(\begin{array}{l}\cos \;\widehat {CHL} = \frac{{C{H^2} + H{L^2} - C{L^2}}}{{2.CH.HL}} = \frac{{{{78}^2} + {{104}^2} - {{49}^2}}}{{2.78.104}} = \frac{{4833}}{{5408}}\\ \Rightarrow \;\widehat {CHL} \approx {26^o}39'40,05''\end{array}\)
Áp dụng hệ quả của định lí cosin trong tam giác HLR, ta có:
\(\begin{array}{l}\cos \;\widehat {LHR} = \frac{{H{L^2} + H{R^2} - L{R^2}}}{{2.HL.HR}} = \frac{{{{104}^2} + {{77}^2} - {{56}^2}}}{{2.104.77}} = \frac{{13609}}{{16016}}\\ \Rightarrow \;\widehat {LHR} \approx {31^o}49'10,4''\\ \Rightarrow \;\widehat {CHR} \approx {58^o}28'50,45''\end{array}\)
Bước 2: Áp dụng định lí cosin \(C{R^2} = H{C^2} + H{R^2} - 2.HC.HR\cos \widehat {CHR}\)
\(\begin{array}{l} \Leftrightarrow C{R^2} = {78^2} + {77^2} - 2.78.77\cos {58^o}28'50,45''\\ \Rightarrow CR \approx 75,72\end{array}\)
Vậy khoảng cách giữa Châu Đốc và Rạch Giá là 75, 72 km.