Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(x\left(x-y\right)+y\left(x+y\right)\)
\(=x^2-xy+xy+y^2\)
\(=x^2+y^2\)
=100
b: \(x\left(x^2-y\right)-x^2\left(x+y\right)+y\left(x^2-x\right)\)
\(=x^3-xy-x^3-x^2y+x^2y-xy\)
\(=-2xy\)

mình biết câu b rồi nhưng câu a thì chưa!
b) x^3(x+y)-x^2(x^2+xy)-x(x-y)
=x^4+x^3y-x^4-x^3y-x^2+xy
=-x^2+xy tại x=10,y=-5 ta có;
=-10^2+10(-5)
= 50

a) x(x-y) + y(x+y) = x^2 - xy + yx + y^2 = x^2 + y^2 = (-6)^2 + 8^2 = 100
b) x(x^2 - y ) - x^2( x + y ) + y(x^2 - x )
= x^3 - xy - x^3 -x^2y+yx^2 - xy
= ( x^3 - x^3 ) + ( x^2 y - x^2 y ) + ( -xy - xy )
= -2xy
Bạn kiểm tra lại đề nhé!

a) \(A=5x\left(4x^2-2x+1\right)-2x\left(10x^2-5x-2\right)\)
\(A=20x^3-10x^2+5x-20x^3+10x^2+4x\)
\(A=9x\)
Thay x = 15 vào, ta có:
\(A=9.15=135\)
b) \(B=5x\left(x-4y\right)-4y\left(y-5x\right)\)
\(B=5x^2-20xy-4y^2+20xy\)
\(B=5x^2-4y\)
Thay \(x=-\frac{1}{5};y=-\frac{1}{2}\) vào, ta có:
\(B=5.\left(-\frac{1}{5}\right)^2-4.\left(-\frac{1}{2}\right)=\frac{11}{5}\)
c) \(C=6xy\left(xy-y^2\right)-8x^2\left(x-y^2\right)-5y^2\left(x^2-xy\right)\)
\(C=6x^2y^2-6xy^3-8x^3+8x^2y^2-5x^2y^2+5xy^3\)
\(C=9x^2y^2-xy^3-8x^3\)
Thay \(x=\frac{1}{2};y=2\) vào, ta có:
\(C=9.\left(\frac{1}{2}\right)^2.2^2-\frac{1}{2}.2^3-8.\left(\frac{1}{2}\right)^3=4\)
d) \(D=\left(3x+5\right)\left(2x-1\right)+\left(4x-1\right)\left(3x+2\right)\)
\(D=6x^2-3x+10x-5+12x^2+8x-3x-2\)
\(D=18x^2+12x-7\)
Ta có: \(\left|2\right|=\orbr{\begin{cases}x=-2\\x=2\end{cases}}\)
+) Với x = -2
\(D=18.\left(-2\right)^2+12.\left(-2\right)-7=41\)
+) Với x = 2
\(D=18.2^2+12.2-7=89\)

Trả lời:
Bài 4:
b, B = ( x + 1 ) ( x7 - x6 + x5 - x4 + x3 - x2 + x - 1 )
= x8 - x7 + x6 - x5 + x4 - x3 + x2 - x + x7 - x6 + x5 - x4 + x3 - x2 + x - 1
= x8 - 1
Thay x = 2 vào biểu thức B, ta có:
28 - 1 = 255
c, C = ( x + 1 ) ( x6 - x5 + x4 - x3 + x2 - x + 1 )
= x7 - x6 + x5 - x4 + x3 - x2 + x + x6 - x5 + x4 - x3 + x2 - x + 1
= x7 + 1
Thay x = 2 vào biểu thức C, ta có:
27 + 1 = 129
d, D = 2x ( 10x2 - 5x - 2 ) - 5x ( 4x2 - 2x - 1 )
= 20x3 - 10x2 - 4x - 20x3 + 10x2 + 5x
= x
Thay x = - 5 vào biểu thức D, ta có:
D = - 5
Bài 5:
a, A = ( x3 - x2y + xy2 - y3 ) ( x + y )
= x4 + x3y - x3y - x2y2 + x2y2 + xy3 - xy3 - y4
= x4 - y4
Thay x = 2; y = - 1/2 vào biểu thức A, ta có:
A = 24 - ( - 1/2 )4 = 16 - 1/16 = 255/16
b, B = ( a - b ) ( a4 + a3b + a2b2 + ab3 + b4 )
= a5 + a4b + a3b2 + a2b3 + ab4 - ab4 - a3b2 - a2b3 - ab4 - b5
= a5 + a4b - ab4 - b5
Thay a = 3; b = - 2 vào biểu thức B, ta có:
B = 35 + 34.( - 2 ) - 3.( - 2 )4 - ( - 2 )5 = 243 - 162 - 48 + 32 = 65
c, ( x2 - 2xy + 2y2 ) ( x2 + y2 ) + 2x3y - 3x2y2 + 2xy3
= x4 + x2y2 - 2x3y - 2xy3 + 2x2y2 + 2y4 + 2x3y - 3x2y2 + 2xy3
= x4 + 2y4
Thay x = - 1/2; y = - 1/2 vào biểu thức trên, ta có:
( - 1/2 )4 + 2.( - 1/2 )4 = 1/16 + 2. 1/16 = 1/16 + 1/8 = 3/16

a) M = (x² + 3xy - 3x³) + (2y³ - xy + 3x³)
= x² + 3xy - 3x³ + 2y³ - xy + 3x³
= x² + (3xy - xy) + (-3x³ + 3x³) + 2y³
= x² + 2xy + 2y³
Tại x = 5 và y = 4
M = 5² + 2.5.4 + 2.4³
= 25 + 40 + 2.64
= 65 + 128
= 193
b) N = x²(x + y) - y(x² - y²)
= x³ + x²y - x²y + y³
= x³ + (x²y - x²y) + y³
= x³ + y³
Tại x = -6 và y = 8
N = (-6)³ + 8³
= -216 + 512
= 296
c) P = x² + 1/2 x + 1/16
= (x + 1/2)²
Tại x = 3/4 ta có:
P = (3/4 + 1/2)² = (5/4)² = 25/16

a) \(x\left(x-y\right)+y\left(x+y\right)=x^2-xy+xy+y^2=x^2+y^2\)
Thay x=-6 ; y=8 ta có:
\(x^2+y^2=\left(-6\right)^2+8^2=36+84=100\)
b)\(x\left(x^2-y\right)-x^2\left(x-y\right)+y\left(x^2-x\right)\\ =x^3-xy-x^3+x^2y+x^2y-xy\\ =2x^2y-2xy\\ =2xy\left(x-1\right)\)
Với x=\(\frac{1}{2}\) ; y=-100 ta có:
\(2xy\left(x-1\right)=2\cdot\frac{1}{2}\cdot\left(-100\right)\cdot\left(\frac{1}{2}-1\right)=-100\cdot-\frac{1}{2}=50\)

1.a) xy + 2y - x2 + 4
= y ( x + 2 ) - ( x2 - 4 ) = y ( x + 2 ) - ( x - 2 ) ( x + 2 ) = ( x + 2 )( y - x + 2 )
b) 2x2 + y2 + 3xy
= ( 2x2 + 2xy ) + ( y2 + xy )
= 2x ( x + y ) + y ( x + y )
= ( x + y ) ( 2x + y )
2.
x - y = 5 \(\Rightarrow\)( x - y )2 = 25 \(\Rightarrow\)x2 + y2 = 25 + 2xy = 25 + 2.3 = 31
A = ( x + y )2 = x2 + y2 + 2xy = 31 + 6 = 37

a) \(A=3x\left(x^2-2x+3\right)-x^2.\left(3x-2\right)+5\left(x^2-x\right)\)
\(=3x^3-6x^2+9x-3x^3+2x^2+5x^2-5x\)
\(=x^2+4x\)
Thay \(x=5\)vào biểu thức ta có: \(A=5^2+4.5=25+20=45\)
b) \(B=x\left(x^2+xy+y^2\right)-y\left(x^2+xy+y^2\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2\right)=x^3-y^3\)
Thay \(x=10\); \(y=-1\)vào biểu thức ta có:
\(B=10^3-\left(-1\right)^3=1000+1=1001\)
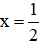 và y = –100;
và y = –100;
a) \(A=x\left(2x-y\right)-2x\left(y-x\right)\)
\(=2x^2-xy-2xy+2x^2\)
\(=4x^2-3xy\)
Tại \(x=5;y=29\) thì: \(A=4.5^2-3.5.29=-335\)
b) \(B=xy\left(x-2\right)-x\left(xy+y\right)\)
\(=x^2y-2xy-x^2y-xy\)
\(=-3xy\)
Tại \(x=4;y=5\)thì: \(B=-3.4.5=-60\)