Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(3333355555.3333377777\)
\(=\left(33333.10^5+55555\right).\left(33333.10^5+77777\right)\)
\(=33333^2.10^{10}+33333.77777.10^5+33333.55555.10^5+55555.77777\)
\(=\left\{{}+\begin{matrix}11110888890000000000\\259254074100000\\185181481500000\\4320901235\end{matrix}\right.\)
\(=11111333329876501235\)
\(Q=3333355555\times3333377777\)
Đặt \(A=33333,B=55555,C=77777\)
\(M=\left(A.10^5+B\right)\left(A.10^5+C\right)=A^2.10^{10}+AC.10^5+AB.10^5+BC\)
Dùng máy tính: \(\left\{{}\begin{matrix}A^2.10^{10}=11110888890000000000\\AC.10^5=259254074100000\\AB.10^5=185181481500000\\BC=4320901235\end{matrix}\right.\)
Ta có bảng sau:
|
\(AB.10^{10}\) |
1 | 1 | 1 | 1 | 0 | 8 | 8 | 8 | 8 | 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
|
\(AC.10^5\) |
2 | 5 | 9 | 2 | 5 | 4 | 0 | 7 | 4 | 1 | 0 | 0 | 0 | 0 | 0 | |||||
|
\(AB.10^5\) |
1 | 8 | 5 | 1 | 8 | 1 | 4 | 8 | 1 | 5 | 0 | 0 | 0 | 0 | 0 | |||||
|
\(BC\) |
4 | 3 | 2 | 0 | 9 | 0 | 1 | 2 | 3 | 5 | ||||||||||
| \(M=\) | 1 | 1 | 1 | 1 | 1 | 3 | 3 | 3 | 3 | 2 | 9 | 8 | 7 | 0 | 5 | 0 | 1 | 2 | 3 | 5 |
Vậy \(Q=3333355555\times3333377777=11111333329870501235\)

ĐKXĐ: \(\sqrt{2}\le x\le\sqrt{2}\)
Ta có : \(2x^2-x+\sqrt{2-x^2}=\frac{7}{2}+\sqrt{2-x}\)
\(\Leftrightarrow4x^2-2x+2\sqrt{2-x^2}=7+2\sqrt{2-x}\)
\(\Leftrightarrow-4\left(2-x^2\right)+2\left(2-x\right)+2\sqrt{2-x^2}-2\sqrt{2-x}-3=0\)
Đặt \(a=\sqrt{2-x^2}\) , \(b=\sqrt{2-x}\) , pt trở thành :
\(-4a^2+2b^2+2a-2b-3=0\)
Tới đây bạn lập ĐENTA rồi tìm mối liên hệ giữa a và b, từ đó suy được pt mới ẩn x.
Vì được dùng máy tính nên bạn tự tìm nghiệm nhé :)

Để kiểm tra 647 có là số nguyên tố không ta chia 647 lần lợt cho 2,3,5,7,11,13,17,19,23,29. Các phép chia đều có dư.
Do đó 647 là số nguyên tố.

a) (Bài đọc thêm SGK trình bày cho các bạn cách sử dụng máy tính CASIO fx-220. Tuy nhiên hiện nay loại máy tính này không còn phổ biến, vậy nên bài làm dưới đây VietJack sẽ trình bày theo cách sử dụng các dòng máy tính CASIO fx – 570 và VINACAL).
+ Nhập hàm số: 
+ Nhập giá trị:

Vậy ta có bảng sau:
| R (cm) | 0,57 | 1,37 | 2,15 | 4,09 |
| S = πR2 | 1,02 | 5,9 | 14,52 | 52,55 |
b) Gọi bán kính mới là R’. Ta có R’ = 3R.
Diện tích mới là :
S ' = π R ' 2 = π ( 3 R ) 2 = π 9 R 2 = 9 π R 2 = 9 S
Vậy khi bán kính tăng lên 3 lần thì diện tích tăng 9 lần.
c) Diện tích hình tròn bằng 79,5
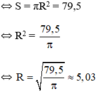

(Bài đọc thêm SGK trình bày cho các bạn cách sử dụng máy tính CASIO fx-220. Tuy nhiên hiện nay loại máy tính này không còn phổ biến, vậy nên bài làm dưới đây VietJack sẽ trình bày theo cách sử dụng các dòng máy tính CASIO fx – 570 và VINACAL).
+ Nhập hàm số: 
+ Nhập giá trị:

Vậy ta có bảng sau:
| R (cm) | 0,57 | 1,37 | 2,15 | 4,09 |
| S = πR2 | 1,02 | 5,9 | 14,52 | 52,55 |

A B C D E
Để dễ hình dung, ta vẽ tam giác ABC vuông tại A, có DE là đường trung trực của cạnh BC ( D thuộc BC, E thuộc AC)
Giả sử góc C = 15 độ , độ dài đoạn AB = 1 (đvđd)
Ta có : Tam giác EBC cân tại E => Góc CBE = Góc C = 15 độ.
Ta có : Góc ABC = 75 độ => Góc ABE = 75 độ - 15 độ = 60 độ.
Suy ra EB = \(\frac{1}{Cos60}=2\) (đvđ.d) ; EA = \(Sin60.EB=\frac{\sqrt{3}}{2}.2=\sqrt{3}\)(đvđ.d) => AC = \(2+\sqrt{3}\)(đvđ.d)
Vì D là trung điểm BC nên ta có CD = DB = \(\frac{BC}{2}=\frac{\sqrt{AB^2+AC^2}}{2}=\frac{\sqrt{1^2+\left(2+\sqrt{3}\right)^2}}{2}=\sqrt{\frac{8+4\sqrt{3}}{4}}=\sqrt{2+\sqrt{3}}\) (đvđ.d)
\(Cos15=\frac{CD}{CE}=\frac{\sqrt{2+\sqrt{3}}}{2}=\frac{\sqrt{2}.\sqrt{4+2\sqrt{3}}}{4}=\frac{\sqrt{2}\left(\sqrt{3}+1\right)}{4}=\frac{\sqrt{6}+\sqrt{2}}{4}\)

3333355555 X 3333377777 = 11111333329876501235
Nhân các chữ số , với nhau , số ở hàng thứ mấy thì lây chừng ấy - 1 số 0