Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nhân các chữ số , với nhau , số ở hàng thứ mấy thì lây chừng ấy - 1 số 0

A) Vì 15 có tận cùng bằng 5 nên khi nhân với 1 số lẻ ( 2003 và 19) thì cũng sẽ có kết quả tận cùng là 5 mà 2003*19*15 = 190281 ( theo đề bài tận cùng là 1). Vậy phép tính làm sai
B) Ta có : 1783+249+65+71 = ...3+...9+...5+...1 có tận cùng là 8 trái với đề bài.Vậy phép tính làm sai

Gọi x là số dương mà đấu bài cho, \(x\in N\)*
Bạn Quân đã chọn số (x – 2) để nhân với x.
Theo đề bài, ta có: x(x – 2) = 120 hay x2 – 2x – 120 = 0
Giải phương trình ta được x = 12 (thỏa mãn)
Theo đầu bài yêu cầu tìm tích của x với x +2
Vậy kết quả đúng phải là: 12.14 = 168

vì tích nhầm của nam la 120 va la 1 so nguyên duong nhân với số bé hơn 2 đv nên ta có
10x12=120;
vậy số nguyên dương là 12 =>tích đúng la:=12x14=168

Gọi số câu trả lời đúng của nhóm là x và câu trả lời sai là y (x;y>0)
Do nhóm phải trả lời 20 câu
\(\Rightarrow x+y=20\)
Số điểm nhóm được cộng từ câu trả lời đúng: \(2x\)
Số điểm bị trừ từ câu trả lời sai: \(y\)
Do nhóm được 28 điểm \(\Rightarrow2x-y=28\)
Ta có hệ pt: \(\left\{{}\begin{matrix}x+y=20\\2x-y=28\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=16\\y=4\end{matrix}\right.\)

Cho ΔABC cân tại A có AB=AC=3cm; BC=4cm
BH=1/2BC=1/2x4=2(cm)
Xét ΔABH vuông tại H có \(\cos B=\dfrac{BH}{AB}=\dfrac{2}{3}\)
nên \(\widehat{B}\simeq48^011'\)
=>Góc cần tìm có số đo là \(1^049'\)

Gọi số mà đề bài đã cho là x, x nguyên dương, x > 2.
Bạn Quân đã chọn số x – 2 để nhân với x.
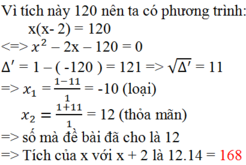
Vậy kết quả đúng phải là 168.
\(3333355555.3333377777\)
\(=\left(33333.10^5+55555\right).\left(33333.10^5+77777\right)\)
\(=33333^2.10^{10}+33333.77777.10^5+33333.55555.10^5+55555.77777\)
\(=\left\{{}+\begin{matrix}11110888890000000000\\259254074100000\\185181481500000\\4320901235\end{matrix}\right.\)
\(=11111333329876501235\)
\(Q=3333355555\times3333377777\)
Đặt \(A=33333,B=55555,C=77777\)
\(M=\left(A.10^5+B\right)\left(A.10^5+C\right)=A^2.10^{10}+AC.10^5+AB.10^5+BC\)
Dùng máy tính: \(\left\{{}\begin{matrix}A^2.10^{10}=11110888890000000000\\AC.10^5=259254074100000\\AB.10^5=185181481500000\\BC=4320901235\end{matrix}\right.\)
Ta có bảng sau:
\(AB.10^{10}\)
\(AC.10^5\)
\(AB.10^5\)
\(BC\)
Vậy \(Q=3333355555\times3333377777=11111333329870501235\)