Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giả sử tam giác ABC có AB = AC = 3cm, BC = 4cm.
Kẻ AH ⊥ BC. Ta có :
![]()
Tam giác ABH vuông tại H nên ta có:
![]()
Sai số là: 50 ° - 48 ° 11 ' = 1 ° 49 '

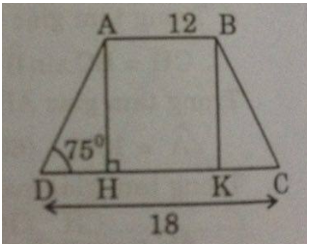
Giả sử hình thang cân ABCD có AB = 12cm, CD = 18cm, ˆD=75∘D^=75∘
Kẻ AH⊥CD,BK⊥CDAH⊥CD,BK⊥CD
Vì tứ giác ABKH là hình chữ nhật nên: AB = HK = 12 (cm)
Ta có: tam giác ADH = tam giác BCK (cạnh huyền, góc nhọn)
Suy ra: DH = CK
Suy ra:
DH=CD–HK2=18–122=3(cm)DH=CD–HK2=18–122=3(cm)
Trong tam giác vuông ADH, ta có:
AH=DH.tgD=3.tg75∘≈11,196(cm)AH=DH.tgD=3.tg75∘≈11,196(cm)
Vậy:
SABCD=AB+CD2.AH≈12+182.11,196=167,94SABCD=AB+CD2.AH≈12+182.11,196=167,94 (cm2).

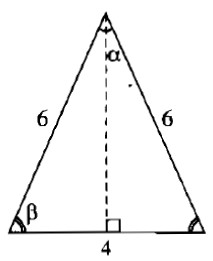
Vì các cạnh của tam giác lần lượt là 4cm, 6cm và 6cm nên tam giác đó là tam giác cân. Góc nhỏ nhất của tam giác là góc đối diện với cạnh 4cm.
Kẻ đường cao từ đỉnh của góc nhỏ nhất. Đường cao chia cạnh đáy thành hai phần bằng nhau mỗi phần 2cm.
Ta có: cosβ=26=13⇒β≈70∘32′cosβ=26=13⇒β≈70∘32′
Suy ra: α=180∘–(β+β)=180∘–2.70∘32'=38∘56′α=180∘–(β+β)=180∘–2.70∘32′=38∘56′
Vậy góc nhỏ nhất của tam giác bằng 38∘56′38∘56′.

Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
Xét ΔBAC vuông tại A có
\(\sin C=\dfrac{AB}{BC}=\dfrac{3}{5}\)
nên \(\widehat{C}=36^052'\)
=>\(\widehat{B}=53^08'\)

Phương pháp giải
Sử dụng: Trong tam giác vuông, cạnh góc vuông bằng cạnh góc vuông kia nhân tan góc đối.

Đặt tên như hình vẽ thì chiều cao của tháp là đoạn BDBD
Xét tam giác ABCABC vuông tại AA có AC=DE=150m;ˆC=200AC=DE=150m;C^=200 nên
AB=150.tan20∘≈54,596(m)AB=150.tan20∘≈54,596(m)
Chiều cao của cột ăng-ten là:
BD=AB+ADBD=AB+AD=54,596+1,5=56,096(m).

a) Trong tam giác vuông BCH, ta có:
CH=BC.sinB^=12.sin60≈10,392 (cm)
Trong tam giác vuông ABC, ta có:
\(A\)=180−(60+40)=80
Trong tam giác vuông ACH, ta có:
\(AC=\dfrac{CH}{sinA}=\dfrac{10,932}{sin80}=10,552\left(cm\right)\)
b) Kẻ AK⊥BCAK⊥BC
Trong tam giác vuông ACK, ta có:
AK=AC.sinC≈10,552.sin40=6,783 (cm)
Vậy SABC=12.AK.BC≈12.6,783.12=40,696 (cm2)

giả sử góc a=135 độ , thì góc d=45 độ.kẻ đường cao ah khi đó góc dah=45 độ vậy tam giác adh cân và vuông.áp dụng pytago ah=6.căn bậc hai của 2.vậy diện tích hbh=15.6 căn bậc 2 của 2=90.căn bậc 2 của 2(cm^2)
vì ABCD là hình bình hành
=> AD // BC ( tính chất )
=> \(\widehat{A}+\widehat{B}=180^0\)( hai góc trong cùng phía)
=> \(\widehat{B}=180^0-110^0=70^0\)
Kẻ AH\(\perp\)BC tại H, ta có tam giác vuông ABH
Xét tam giác vuông ABH, có:
AH=AB*sin B=12*sin 70 độ
\(AH\approx11,276\)(cm)
ta có: AD=BC ( ABCD là hình chữ nhật )
\(\Rightarrow S_{ABCD}=AH\cdot BC\approx11,276\cdot15=169,14\)(\(cm^2\))

Không có góc nhọn nào như vậy bởi nếu x là góc nhọn thì \(\sin x< =1;\cos x< =1\)

\(\sin39^013'=0,6322\)
\(\cos52^018'=0,6115\)
\(\tan13^020'=0,2370\)
\(\cot10^017'=5,5118\)
\(\sin54^0=0,8090\)
\(\cos45^0=0,7071\)
Cho ΔABC cân tại A có AB=AC=3cm; BC=4cm
BH=1/2BC=1/2x4=2(cm)
Xét ΔABH vuông tại H có \(\cos B=\dfrac{BH}{AB}=\dfrac{2}{3}\)
nên \(\widehat{B}\simeq48^011'\)
=>Góc cần tìm có số đo là \(1^049'\)