K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TC
50
HT
0
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 4 2020
Do \(x< 2\) nên x chỉ tiến tới 2 từ phía trái
Do đó hàm số chỉ có giới hạn trái tại điểm x=2 (giới hạn bằng dương vô cực)
TC
46
NT
1
12 tháng 5 2016
Đặt \(t=x-10\Rightarrow\begin{cases}x=t+10\\x\rightarrow t;t\rightarrow0\end{cases}\)
\(\Rightarrow L=\lim\limits_{t\rightarrow0}\frac{lg\left(t+10\right)-lg10}{t}=\lim\limits_{t\rightarrow0}\frac{lg\left(\frac{t+10}{10}\right)}{t}=\lim\limits_{t\rightarrow0}\left[\frac{lg\left(1+\frac{t}{10}\right)}{\frac{t}{10}}.\frac{1}{10}\right]=\frac{1}{10}\)
12 tháng 5 2016
\(L=\lim\limits_{x\rightarrow+\infty}\left(\frac{x}{1+x}\right)^x\)
Ta có : \(L=\lim\limits_{x\rightarrow+\infty}\left(\frac{x}{1+x}\right)^x=\lim\limits_{x\rightarrow+\infty}\left(1-\frac{1}{1+x}\right)^x\)
Đặt \(-\frac{1}{1+x}=\frac{1}{t}\Rightarrow\begin{cases}x=-\left(1+t\right)\\x\rightarrow+\infty;t\rightarrow-\infty\end{cases}\)
\(\Rightarrow L=\lim\limits_{t\rightarrow-\infty}\left(1+\frac{1}{t}\right)^{-\left(1+t\right)}=\lim\limits_{t\rightarrow-\infty}\frac{1}{\left(1+\frac{1}{t}\right)^{1+t}}=\lim\limits_{t\rightarrow-\infty}\frac{1}{\left(1+\frac{1}{t}\right)\left(1+\frac{1}{t}\right)^t}=\frac{1}{1.e}=\frac{1}{e}\)
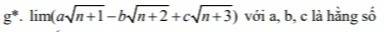
\(\lim\limits_{x\rightarrow+\infty}\left(3x-\sqrt{9x^2+4x}\right)=\lim\limits_{x\rightarrow+\infty}\dfrac{-4x}{3x+\sqrt{9x^2+4x}}=\lim\limits_{x\rightarrow+\infty}\dfrac{-4}{3+\sqrt{9+\dfrac{4}{x}}}=-\dfrac{2}{3}\)
\(\lim\limits_{x\rightarrow+\infty}\left(2x-\sqrt[3]{8x^3+x}\right)=\lim\limits_{x\rightarrow+\infty}\dfrac{-x}{4x^2+2x\sqrt[3]{8x^3+x}+\sqrt[3]{8x^3+x}}=0\)
\(\lim\limits_{x\rightarrow-\infty}\left(2x+\sqrt[3]{8x^3+x}\right)=2x\left(1+\sqrt[3]{1+\dfrac{1}{8x^2}}\right)=-\infty.2=-\infty\)