Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Tính giá trị của biểu thức :
a) \(2\sin30^0+3\cos45^0-\sin60^0\)
b) \(2\cos30^0+3\sin45^0-\cos60^0\)

a)
\(2sin30+3sin45^o-sin60^o=2.\dfrac{1}{2}+3.\dfrac{\sqrt{2}}{2}-\dfrac{\sqrt{3}}{2}\)\(=\dfrac{2+3\sqrt{2}-\sqrt{3}}{2}\).
b)\(2cos30^o+3sin45^o-cos60^o=2.\dfrac{\sqrt{3}}{2}+3.\dfrac{\sqrt{2}}{2}-\dfrac{1}{2}\)\(=\dfrac{2\sqrt{3}+3\sqrt{2}-1}{2}\).

a: \(=\dfrac{a^2-b^2}{\dfrac{\sqrt{2}}{2}a+b\cdot0-2a\cdot0}=\dfrac{a^2-b^2}{\dfrac{\sqrt{2}}{2}a}\)
b: \(=3a+b-a=2a+b\)

Toàn góc quen thuộc, cứ ném vào máy tính cho nó xử thôi:
\(P=\frac{\sqrt{3}.\frac{\sqrt{3}}{3}-\frac{1}{2}.\sqrt{3}-2\sqrt{2}.\frac{\sqrt{2}}{2}}{\sqrt{6}.1.\frac{\sqrt{2}}{2}.\frac{\sqrt{3}}{2}}=-\frac{2+\sqrt{3}}{3}\)

Chú ý rằng: sin450 = cos450, sin400 = cos500, sin500 = cos400
Ta được:
\(\dfrac{\cos50^0-\cos45^0+\cos50^0}{\cos40^0-\cos45^0+\cos50^0}-\dfrac{6\times3\left(\dfrac{\sqrt{3}}{3}+\tan15^0\right)}{3\left(1-\dfrac{\sqrt{3}}{3}\tan15^0\right)}\)
\(=1-6\left(\dfrac{\tan30^0+\tan15^0}{1-\tan30^0\times\tan15^0}\right)\)
\(=1-6\tan45^0=-5\)

Ta có cos45 độ + sin45 độ=√2/2+√2/2=√2
Chọn (B).

Ta có \(\sqrt{8a^2+56}=\sqrt{8\left(a^2+7\right)}=2\sqrt{2\left(a^2+ab+2bc+2ca\right)}\)
\(=2\sqrt{2\left(a+b\right)\left(a+2c\right)}\le2\left(a+b\right)+\left(a+2c\right)=3a+2b+2c\)
Tương tự \(\sqrt{8b^2+56}\le2a+3b+2c;\)\(\sqrt{4c^2+7}=\sqrt{\left(a+2c\right)\left(b+2c\right)}\le\frac{a+b+4c}{2}\)
Do vậy \(Q\ge\frac{11a+11b+12c}{3a+2b+2c+2a+3b+2c+\frac{a+b+4c}{2}}=2\)
Dấu "=" xảy ra khi và chỉ khi \(\left(a,b,c\right)=\left(1;1;\frac{3}{2}\right)\)
a) \(P=1957\)
b) \(S=19.\)
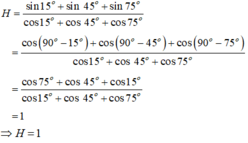
Ai giải giúp mik vs