Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

M = 1/1.2.3 + 1/2.3.4 + 1/3.4.5 + ... + 1/10.11.12
M = 1/2.(2/1.2.3 + 2/2.3.4 + 2/3.4.5 + ... + 2/10.11.12)
M = 1/2.(1/1.2 - 1/2.3 + 1/2.3- 1/3.4 + 1/3.4 - 1/4.5 + ... + 1/10.11 - 1/11.12)
M = 1/2.(1/1.2 - 1/11.12)
M = 1/4 - 1/264
M = 65/264

\(M=\frac{1}{2}\left(\frac{1}{1.2}-\frac{1}{2.3}+\frac{1}{2.3}-\frac{1}{3.4}+...+\frac{1}{10.11}-\frac{1}{11.12}\right)\)
\(M=\frac{1}{2}\left(\frac{1}{1.2}-\frac{1}{11.12}\right)\)
\(M=\frac{1}{2}.\left(\frac{1}{2}-\frac{1}{132}\right)\)

\(D=\frac{1}{1\cdot2\cdot3}+\frac{1}{2\cdot3\cdot4}+\frac{1}{3\cdot4\cdot5}+...+\frac{1}{10\cdot11\cdot12}\)
\(D=\frac{1}{2}\left(\frac{2}{1\cdot2\cdot3}+\frac{2}{2\cdot3\cdot4}+\frac{2}{3\cdot4\cdot5}+...+\frac{2}{10\cdot11\cdot12}\right)\)
\(D=\frac{1}{2}\left(\frac{1}{1\cdot2}-\frac{1}{2\cdot3}+\frac{1}{2\cdot3}-\frac{1}{3\cdot4}+\frac{1}{3\cdot4}-\frac{1}{4\cdot5}+...+\frac{1}{10\cdot11}-\frac{1}{11\cdot12}\right)\)
\(D=\frac{1}{2}\left(\frac{1}{2}-\frac{1}{132}\right)=...\)
\(D=\frac{1}{1.2.3}+\frac{1}{2.3.4}+\frac{1}{3.4.5}+...+\frac{1}{10.11.12}\)
\(D=\left(\frac{2}{1.2.3}+\frac{2}{2.3.4}+\frac{2}{3.4.5}+...+\frac{2}{10.11.12}\right).\frac{1}{2}\)
\(D=\left(\frac{1}{1.2}-\frac{1}{2.3}+\frac{1}{2.3}-\frac{1}{3.4}+\frac{1}{3.4}-\frac{1}{4.5}+...+\frac{1}{10.11}-\frac{1}{11.12}\right).\frac{1}{2}\)
\(D=\left(\frac{1}{1.2}-\frac{1}{11.12}\right).\frac{1}{2}\)
\(D=\frac{65}{132}.\frac{1}{2}\)
\(D=\frac{65}{264}\)

2A=2(1/1.2.3+1/2.3.4+...+1/98.99.100)
2A=1/1.2-1/2.3+1/2.3-1/3.4+1/3.4-...+1/98.99-1/99.100
2A=1/1.2-1/99.100
2A=4949/9900
A=4949/9900:2
A=4949/19800
Vậy A=4949/198000

\(2M=2\cdot\left(\frac{1}{1\cdot2\cdot3}+\frac{1}{2\cdot3\cdot4}+.....+\frac{1}{10\cdot11\cdot12}\right)\)
\(2M=\frac{2}{1\cdot2\cdot3}+\frac{2}{2\cdot3\cdot4}+.....+\frac{2}{10\cdot11\cdot12}\)
\(2M=\frac{1}{1\cdot2}-\frac{1}{2\cdot3}+\frac{1}{2\cdot3}-\frac{1}{3\cdot4}+.....+\frac{1}{10\cdot11}-\frac{1}{11\cdot12}\)
\(2M=\frac{1}{1\cdot2}-\frac{1}{11\cdot12}\)
\(2M=\frac{1}{2}-\frac{1}{132}\)
\(2M=\frac{66}{132}-\frac{1}{132}\)
\(2M=\frac{65}{132}\)
\(M=\frac{65}{132}:2\)
\(M=\frac{65}{264}\)

Ta có : \(B=\frac{1}{1.2.3}+\frac{1}{2.3.4}+...+\frac{1}{18.19.20}\)
\(\Leftrightarrow2B=\frac{2}{1.2.3}+\frac{2}{2.3.4}+...+\frac{2}{18.19.20}\)
\(=\frac{1}{1.2}-\frac{1}{2.3}+\frac{1}{2.3}-\frac{1}{3.4}+....+\frac{1}{18.19}-\frac{1}{19.20}\)
\(=\frac{1}{2}-\frac{1}{19.20}=\frac{189}{380}\)
\(\Rightarrow B=\frac{189}{760}\)
\(B=\frac{1}{1.2.3}+\frac{1}{2.3.4}+\frac{1}{3.4.5}+...+\frac{1}{18.19.20}\)
\(=\frac{1}{2}\left(\frac{1}{1.2}-\frac{1}{2.3}\right)+\frac{1}{2}\left(\frac{1}{2.3}-\frac{1}{3.4}\right)+...+\frac{1}{2}\left(\frac{1}{18.19}-\frac{1}{19.20}\right)\)
\(=\frac{1}{2}\left(\frac{1}{1.2}-\frac{1}{2.3}+\frac{1}{2.3}-\frac{1}{3.4}+...+\frac{1}{18.19}-\frac{1}{19.20}\right)\)
\(=\frac{1}{2}\left(\frac{1}{1.2}-\frac{1}{19.20}\right)\)
\(=\frac{1}{2}.\left(\frac{1}{2}-\frac{1}{380}\right)\)
\(=\frac{1}{2}.\frac{189}{380}=\frac{189}{760}\)

Ta có :
\(\dfrac{1}{1.2}-\dfrac{1}{2.3}=\dfrac{3}{1.2.3}-\dfrac{1}{1.2.3}=\dfrac{2}{1.2.3}\)
\(\dfrac{1}{2.3}-\dfrac{1}{3.4}=\dfrac{4}{2.3.4}-\dfrac{2}{2.3.4}=\dfrac{2}{2.3.4}\)
...
Do đó :
\(\dfrac{1}{1.2.3}=\dfrac{1}{2}\left(\dfrac{1}{1.2}-\dfrac{1}{2.3}\right)\)
\(\dfrac{1}{2.3.4}=\dfrac{1}{2}\left(\dfrac{1}{2.3}-\dfrac{1}{3.4}\right)\)
Vậy :
\(M=\dfrac{1}{2}\left(\dfrac{1}{1.2}-\dfrac{1}{2.3}+\dfrac{1}{2.3}-\dfrac{1}{3.4}+\dfrac{1}{3.4}-\dfrac{1}{4.5}+...+\dfrac{1}{10.11}-\dfrac{1}{11.12}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{1}{1.2}-\dfrac{1}{11.12}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{1}{2}-\dfrac{1}{132}\right)\)
\(=\dfrac{1}{2}.\dfrac{65}{132}=\dfrac{65}{264}\)

Xét ct trước :D
\(\frac{2}{\left[\left(n-1\right)n\left(n+1\right)\right]}=\frac{1}{\left[\left(n-1\right)n\right]}-\frac{1}{\left[n\left(n+1\right)\right]}\)
Sau khi xét ct rồi thì /Bùm/ Ta được:
\(2M=\frac{2}{1.2.3}+\frac{2}{2.3.4}+\frac{2}{3.4.5}+...+\frac{2}{10.11.12}\)
\(=\frac{1}{1.2}-\frac{1}{2.3}+\frac{1}{2.3}-\frac{1}{3.4}+\frac{1}{3.4}-\frac{1}{4.5}+...+\frac{1}{10.11}+\frac{1}{11.12}\)
\(=\frac{1}{1.2}-\frac{1}{11.12}\)
\(=\frac{65}{132}\)
\(\Rightarrow M=\frac{65}{264}\)
Ok rồi nhé :)
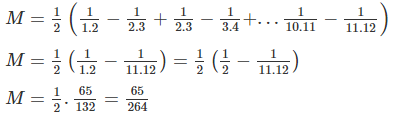
Giải:
Ta có nhận xét:
\(\frac{1}{1.2}-\frac{1}{2.3}=\frac{3-1}{1.2.3}=\frac{2}{1.2.3}\)
\(\frac{1}{2.3}-\frac{1}{3.4}=\frac{4-2}{2.3.4}=\frac{2}{2.3.4}\)
=>\(\frac{1}{1.2.3}=\frac{1}{3}\left(\frac{1}{1.2}-\frac{1}{2.3}\right)\)
\(\frac{1}{2.3.4}=\frac{1}{2}\left(\frac{1}{2.3}-\frac{1}{3.4}\right)\)
Do đó M=\(\frac{1}{2}\left(\frac{1}{1.2}-\frac{1}{2.3}+\frac{1}{2.3}+\frac{1}{3.4}+....+\frac{1}{10.11}-\frac{1}{11.12}\right)\)
=\(\frac{1}{2}\left(\frac{1}{1.2}-\frac{1}{11.12}\right)=\frac{1}{2}-\frac{1}{11.12}\)
=\(\frac{1}{2}.\frac{65}{132}=\frac{65}{124}\)
Vậy M=65/124
M=\(\frac{65}{124}\)