Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

đặt S=1.2.3+2.3.4+....+47.48.49
4S=1.2.3.(4-0)+2.3.4.(5-1)+...+47.48.49.(50-46)
4S=1.2.3.4-1.2.3+2.3.4.5-1.2.3.4+....+47.48.49.50-46.47.48.49
4S=47.48.49.50-1.2.3
S=(47.48.49.50-1.2.3):4


\(M=\frac{1}{1.2.3}+\frac{1}{2.3.4}+\frac{1}{3.4.5}+.....+\frac{1}{10.11.12}\)
\(M=\frac{1}{2}-\frac{1}{11.12}\)
\(M=\frac{65}{132}\)
Ngắn gọn , xúc tích !!! :))

\(M=\frac{1}{1.2}-\frac{1}{2.3}+\frac{1}{2.3}-\frac{1}{3.4}+...+\frac{1}{10.11}-\frac{1}{11.12}\)
\(=\frac{1}{2}-\frac{1}{11.12}\)
\(=\frac{65}{132}\)
Ta có nhận xét: 1/1.2 - 1/2.3 = 3-1/1.2.3 = 2/1.2.3
1/2.3 - 1/3.4 = 4-2/2.3.4 = 2/2.3.4
Suy ra: 1/1.2.3 = 1/2(1/1.2 - 1/2.3)
1/2.3.4 = 1/2(1/2.3 -1/3.4)
Do đó: M = 1/2(1/1.2-1/2.3 + 1/2.3 -1/3.4 + ... + 1/10.11 -1/11.12)
= 1/2(1/1.2 - 1/11.12) = 1/2(1/2-11/12 )
= 1/2.65/132 = 65/264
Phức tạp lắm

Giải:
Ta có nhận xét:
\(\frac{1}{1.2}-\frac{1}{2.3}=\frac{3-1}{1.2.3}=\frac{2}{1.2.3}\)
\(\frac{1}{2.3}-\frac{1}{3.4}=\frac{4-2}{2.3.4}=\frac{2}{2.3.4}\)
=>\(\frac{1}{1.2.3}=\frac{1}{3}\left(\frac{1}{1.2}-\frac{1}{2.3}\right)\)
\(\frac{1}{2.3.4}=\frac{1}{2}\left(\frac{1}{2.3}-\frac{1}{3.4}\right)\)
Do đó M=\(\frac{1}{2}\left(\frac{1}{1.2}-\frac{1}{2.3}+\frac{1}{2.3}+\frac{1}{3.4}+....+\frac{1}{10.11}-\frac{1}{11.12}\right)\)
=\(\frac{1}{2}\left(\frac{1}{1.2}-\frac{1}{11.12}\right)=\frac{1}{2}-\frac{1}{11.12}\)
=\(\frac{1}{2}.\frac{65}{132}=\frac{65}{124}\)
Vậy M=65/124

a, A = 1.2.3 . 4 + 2.3.4 . 4 + 3.4.5 . 4 + 4.5.6 . 4
= 4.(1.2.3+2.3.4+3.4.5+4.5.6) = 4.B
=> A gấp 4 lần B
b, A= (1.2.3. .... .35 + 1.2.3 . ..... .36) : 37 = (1.2.3. .... .35).(1+36):37 = 1.2.3 . .... .35 = 35 giai thừa = B
=> A = B

Ta có :
\(\dfrac{1}{1.2}-\dfrac{1}{2.3}=\dfrac{3}{1.2.3}-\dfrac{1}{1.2.3}=\dfrac{2}{1.2.3}\)
\(\dfrac{1}{2.3}-\dfrac{1}{3.4}=\dfrac{4}{2.3.4}-\dfrac{2}{2.3.4}=\dfrac{2}{2.3.4}\)
...
Do đó :
\(\dfrac{1}{1.2.3}=\dfrac{1}{2}\left(\dfrac{1}{1.2}-\dfrac{1}{2.3}\right)\)
\(\dfrac{1}{2.3.4}=\dfrac{1}{2}\left(\dfrac{1}{2.3}-\dfrac{1}{3.4}\right)\)
Vậy :
\(M=\dfrac{1}{2}\left(\dfrac{1}{1.2}-\dfrac{1}{2.3}+\dfrac{1}{2.3}-\dfrac{1}{3.4}+\dfrac{1}{3.4}-\dfrac{1}{4.5}+...+\dfrac{1}{10.11}-\dfrac{1}{11.12}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{1}{1.2}-\dfrac{1}{11.12}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{1}{2}-\dfrac{1}{132}\right)\)
\(=\dfrac{1}{2}.\dfrac{65}{132}=\dfrac{65}{264}\)
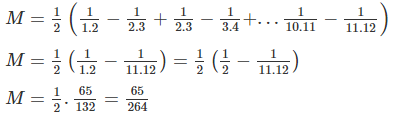
\(M=1.2.3+2.3.4+3.4.5+...+47.48.49\)
\(4M=1.2.3.4+2.3.4.\left(5-1\right)+3.4.5.\left(6-2\right)+...+47.48.49.\left(50-46\right)\)
\(=1.2.3.4+2.3.4.5-1.2.3.4+3.4.5.6-2.3.4.5+...+47.48.49.50-46.47.48.49\)
\(=47.48.49.50\)
\(M=\frac{47.48.49.50}{4}=1381800\)