Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
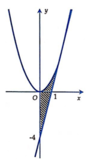
Ta có y ' = 2 x .
Phương trình tiếp tuyến của đường cong y = x 2 tại điểm có hoành độ bằng 2 có dạng y = 2.2 x − 2 + 2 2 ⇔ y = 4 x − 4 .
Hình phẳng cần tính diện tích là phần kẻ sọc.
Vậy S = ∫ 0 2 x 2 − 4 x + 4 d x = 8 3 . Ta chọn B.

Đáp án B.
Phương trình tiếp tuyến của (P) tại điểm M:
y = 4 x − 1 + 2 = 4 x − 2.
S = ∫ 0 1 2 x 2 − 4 x + 2 d x = 2 3 .

Thể tích vật thể tròn xoay cần tìm là
V = π ∫ 0 2 x 2 dy = π ∫ 0 2 y 4 dy = 32 π 5
Đáp án B

Chọn C.
Tiếp tuyến của (P) tại M(1;0) là d: y = 2x - 2
Phương trình hoành độ giao điểm x 2 - 1 = 2 x - 2 ⇔ x 2 - 2 x + 1 = 0 ⇔ x = 1 .
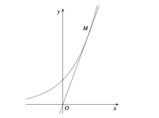
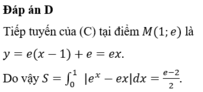




HD: Phương trình tiếp tuyến là y = 4x - 3.
Phương trình hoành độ giao điểm
x2 +1 = 4x - 3 ⇔ x2 - 4x + 4 = 0 ⇔ x = 2.
Do đó diện tích phải tìm là: