Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu hỏi của NGUUYỄN NGỌC MINH - Toán lớp 9 - Học toán với OnlineMath

Giả sử \(\frac{a^2+b^2}{ab-1}=k\left(k\in Z\right)\). Ta sẽ đi tìm k và chứng minh k là số nguyên tố.
Đặt \(m=a+b;n=a-b\), ta có \(\frac{a^2+b^2}{ab-1}=k\Rightarrow\frac{m^2+n^2}{m^2-n^2-4}=\frac{k}{2}\)
TH1: Nếu trong a và b có một số chẵn, một số lẻ:
Khi đó k là số lẻ. Đặt \(d=\left(m^2+n^2;m^2-n^2-4\right)\Rightarrow d=\left(2m^2-4,2n^2+4\right)\)
\(\Leftrightarrow\) d | 2(m2 + n2) = 4(a2 + b2)
Mà \(\hept{\begin{cases}m^2+n^2=kd\\m^2-n^2-4=2d\end{cases}}\)
\(\Leftrightarrow2x^2-4=d\left(k+2\right)\Rightarrow\) d chia hết 2.
Lại có a2 + b2 là số lẻ nên d = 2 hoặc d = 4.
Thay vào hệ bên trên và giả thiết thì (a,b) = (-2;-1) hoặc (2;1). Khi đó k = 5 và nó là số nguyên tố.
TH2: Nếu cả a và b đều lẻ
\(\Rightarrow a=2k+1;b=2h+1\Rightarrow k=\frac{2\left(k^2+h^2+k+h\right)+1}{2kh+k+h}\) là số lẻ.
Tương tự như bên trên ta có d | 4(a2 + b2) = 8(2k2 + 2h2 + 2k + 2h + 1)
Và 2m2 - 4 = (k+2)d \(\Rightarrow d⋮2\Rightarrow d\in\left\{2;4;8\right\}\)
Thế vào hệ ta cũng tìm được (a;b) = (3;1) hoặc (-3;-10 và k = 5.
Vậy k luôn bằng 5 và nó là số nguyên tố.

Bài cuối có Max nữa nhé, cần thì ib mình làm cho.
Giả sử \(c=min\left\{a;b;c\right\}\Rightarrow c\le1< 2\Rightarrow2-c>0\)
Ta có:\(P=ab+bc+ca-\frac{1}{2}abc=\frac{ab}{2}\left(2-c\right)+bc+ca\ge0\)
Đẳng thức xảy ra tại \(a=3;b=0;c=0\) và các hoán vị
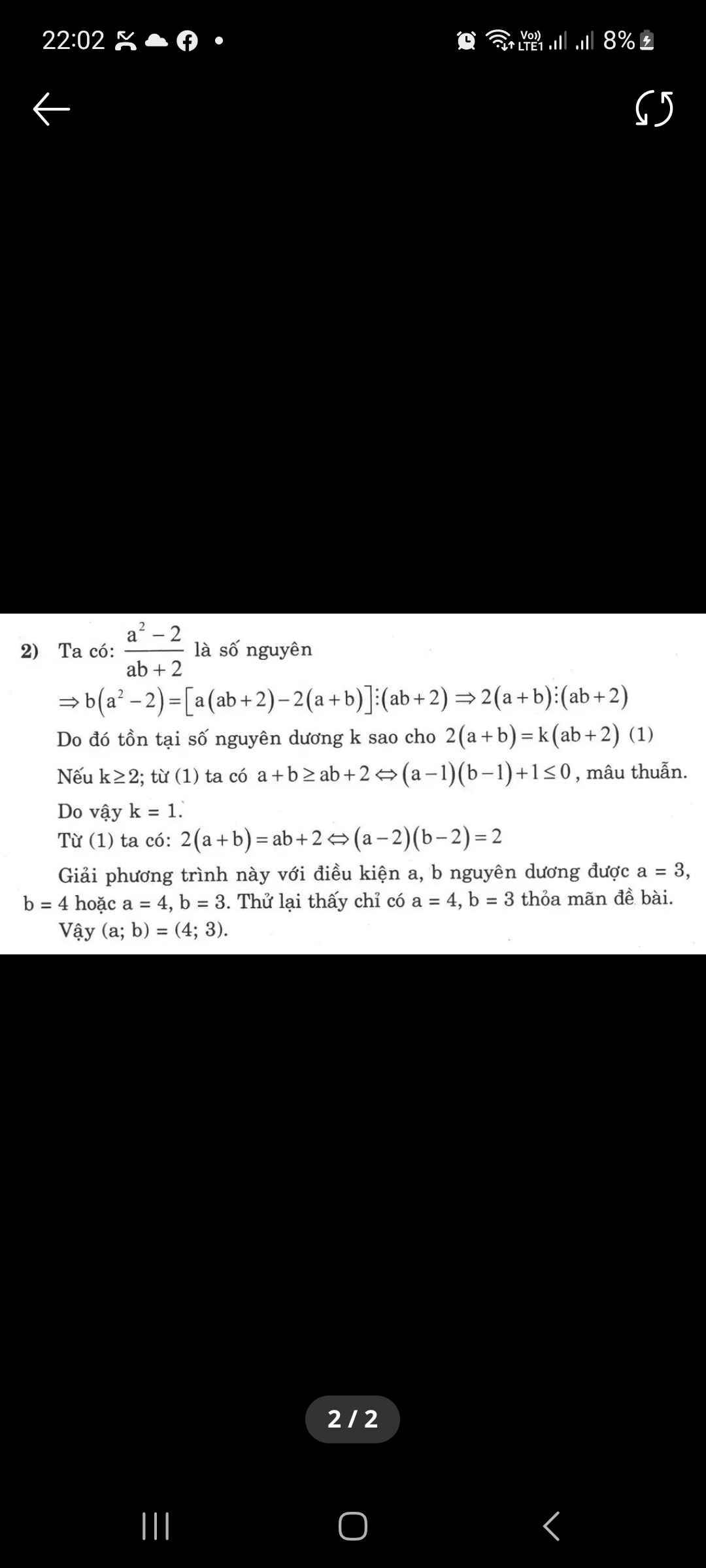
Ta có \(b\left(a^2-2\right)=a\left(ab+2\right)-2\left(a+b\right)\). Do \(a^2-2\vdots ab+2\) nên \(2\left(a+b\right)\vdots ab+2\to ab+2\le2a+2b\to\left(a-2\right)\left(b-2\right)\le2\).
Với \(a=1\to-\frac{1}{b+2}\in Z\), loại
Với \(a=2\to\frac{4}{2b+2}\in Z\to2b+2=4\to b=1\)
Với \(a=3\to\frac{7}{3b+2}\in Z\to3b+2=7\to\) loại
Với \(a=4\to\frac{14}{4b+2}\in Z\to4b+2=14\to b=3.\)
Với \(a\ge5\to b-2\le\frac{2}{a-2}<1\to b\le2\to b=1,2\). Với \(b=1\to\frac{a^2-2}{a+2}\in Z\to a-2+\frac{2}{a+2}\in Z\to a+2=2\to\) loại.
Nếu \(b=2\to\frac{a^2-2}{2a+2}\in Z\to\frac{a^2-2}{a+1}\in Z\to\frac{3}{a+1}\in Z\to a+1=3\to\) loại.
Vậy các cặp số \(\left(a,b\right)\) nguyên dương thoả mãn là \(\left(2,1\right);\left(4,3\right).\)
đua ha đô kho qua chung