Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
Đặt ![]() ,
, ![]() thì
thì ![]() .
.
Ta có:
![]()
![]()
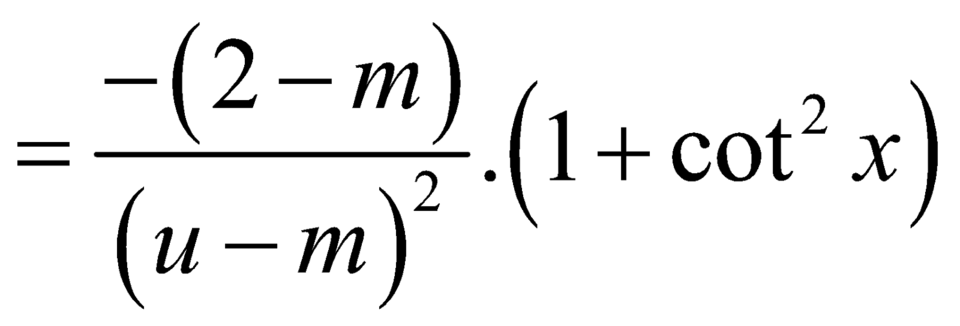 .
.
Hàm số đồng biến trên ![]()
![]()
với mọi ![]() thuộc
thuộc ![]() hay
hay 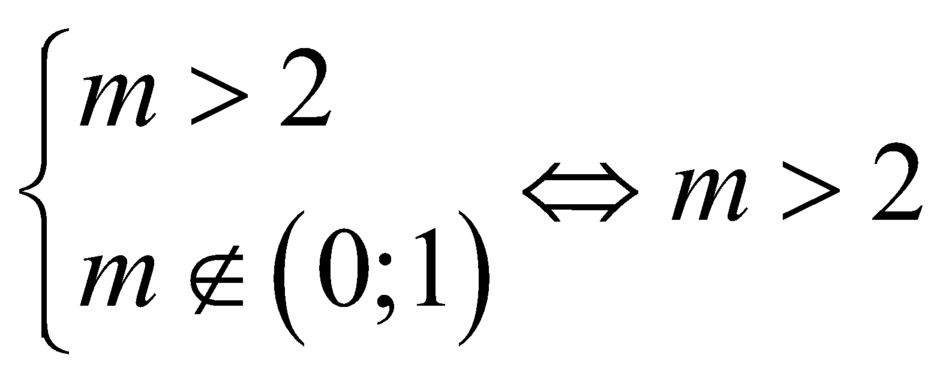 .
.

Đặt \(2^{cotx}=t\Rightarrow t\in(-\infty;1]\)
Để ý rằng \(cotx\) nghịch biến trên khoảng đã cho nên \(f\left(x\right)\) đồng biến \(\Leftrightarrow f\left(t\right)=t^3+\left(m-3\right)t+3m-2\) nghịch biến trên \((-\infty;1]\)
Quy về 1 bài toán đồng biến - nghịch biến bình thường của hàm bậc 3
Ủa, ngáo rồi, đặt \(2^{cotx}=t\) chứ có phải \(cotx=t\) đâu, vậy \(t\in(0;2]\) mới đúng (cách làm vẫn y như trên, chỉ khác khoảng của t)

1.
\(y'=m-3cos3x\)
Hàm đồng biến trên R khi và chỉ khi \(m-3cos3x\ge0\) ; \(\forall x\)
\(\Leftrightarrow m\ge3cos3x\) ; \(\forall x\)
\(\Leftrightarrow m\ge\max\limits_{x\in R}\left(3cos3x\right)\)
\(\Leftrightarrow m\ge3\)
2.
\(y'=1-m.sinx\)
Hàm đồng biến trên R khi và chỉ khi:
\(1-m.sinx\ge0\) ; \(\forall x\)
\(\Leftrightarrow1\ge m.sinx\) ; \(\forall x\)
- Với \(m=0\) thỏa mãn
- Với \(m< 0\Rightarrow\dfrac{1}{m}\le sinx\Leftrightarrow\dfrac{1}{m}\le\min\limits_R\left(sinx\right)=-1\)
\(\Rightarrow m\ge-1\)
- Với \(m>0\Rightarrow\dfrac{1}{m}\ge sinx\Leftrightarrow\dfrac{1}{m}\ge\max\limits_R\left(sinx\right)=1\)
\(\Rightarrow m\le1\)
Kết hợp lại ta được: \(-1\le m\le1\)

Đáp án A
Hàm số đồng biến trên ![]()
![]()
![]() .
.
Xét hàm số ![]()
![]() .
.
Khi đó ![]() .
.
Bảng biến thiên:
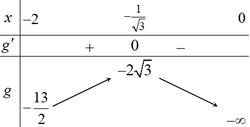
Từ bảng biến thiên suy ra các giá trị cần tìm của m là ![]() .
.

Chọn D
Đặt ![]() ,
, ![]() thì
thì ![]() . Ta có:
. Ta có:
![]()
![]()
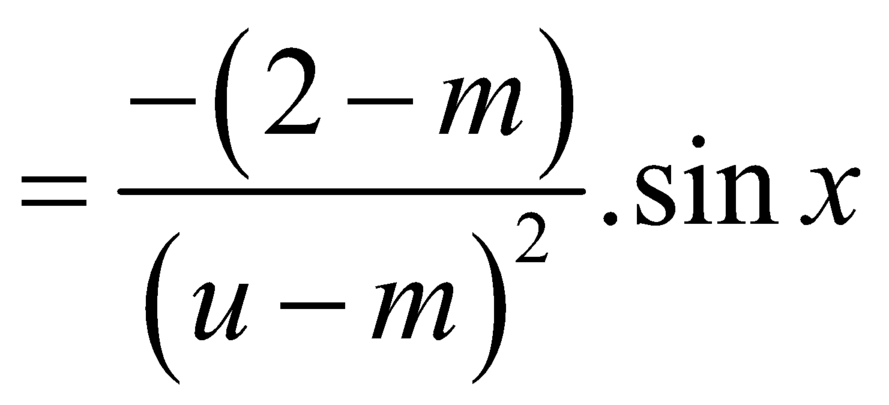 .
.
Vì ![]() nên ycbt
nên ycbt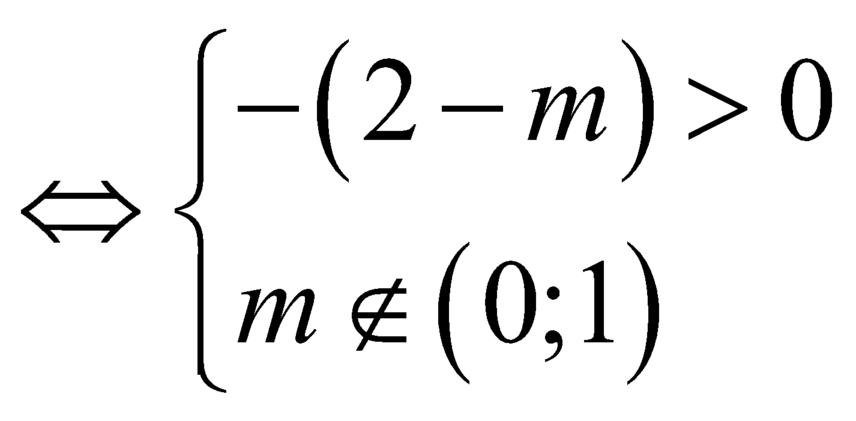 .
.
Đến đây giải được: ![]() .
.

y'= \(4x^3-4\left(m-1\right)x\)
Để hàm số đồng biến trên khoảng (1;3) thì \(y'\left(x\right)\ge0,\forall x\in\left(1;3\right)\)
\(\Leftrightarrow x^2-\left(m-1\right)\ge0,\forall x\in\left(1;3\right)\)
\(\Leftrightarrow m-1\le x^2,\forall x\in\left(1;3\right)\)
\(\Rightarrow m-1\le1\Leftrightarrow m\le2\)
Vậy \(m\in\) (−\(\infty\);2]

Đáp án D.
Ta có
y ' = 3 e 3 x - m - 1 e x . 2017 2018 e 3 x - m - 1 e x + 1 . ln 2017 2018
Để hàm số đồng biến trên (1;2)
⇔ y ' ≥ 0 ; ∀ x ∈ 1 ; 2 ⇔ 3 e 3 x - m - 1 e x ≤ 0 ; ∀ x ∈ 1 ; 2 .
⇔ 3 e 2 x - m + 1 ≤ 0 ; ∀ x ∈ 1 ; 2
⇔ m - 1 ≥ 3 e 2 x ; ∀ x ∈ 1 ; 2
⇔ m ≥ 3 e 4 + 1 .