Q
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
17 tháng 8 2023
Vì cộng thêm vào tử số 4 đơn vị và giữ nguyên mẫu thì được phân số có giá trị bằng 1 nên mẫu số hơn tử số 4 đơn vị
Vì giữ nguyên tử số và cộng vào mẫu số 3 đơn vị nên mẫu số lúc sau hơn tử số lúc đầu là: 4 + 3 = 7
Theo bài ra ta có sơ đồ:
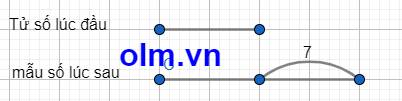
Theo sơ đồ ta có: 7:(2-1) =7
Mẫu số lúc đầu là: 7 + 4 = 11
Phân số cần tìm là \(\dfrac{7}{11}\)
đs..
CC
22 tháng 9 2016
1/Phân số đó có mẫu lớn hơn tử là 2.
Chuyển 5 đơn vị từ tử xuống mẫu có nghĩa là mẫu mới lơn hơn tử mới:
2+5+5 =12
( 2 là hiệu cũ bớt ở tự là tăng hiệu thêm 5 và thêm mẫu 5 nửa)
Tử số mới: 12:(2-1)x1=12
Mẫu số mới: 12+12=24
Tử số cũ: 12+5=17
Mẫu số cũ: 17+2=19
Phân số đó là 17/19
27 tháng 5 2017
Chuyển 1 đơn vị từ mẫu số lên tử số thì được phân số bằng 1
=> Tử số kém mẫu số 2 đơn vị
Nếu chuyển 7 đơn vị từ tử số xuống mẫu số => tử số bớt đi 7 và mẫu số tăng thêm 7
=> tử số mới kém mẫu số mới là 2 + 7x2 = 16 đơn vị
Tìm 2 số (mẫu số mới, tử số mới) có hiệu 16 và tỉ lệ 3/2
Mẫu số mới 3 phần thì Tử số mới 2 phần, Hiệu sẽ là 3 - 2 = 1 phần ứng với 16
=> Mẫu số mới là: 16 x 3 = 48; Tử số mới là: 16 x 2 = 32
=> Mẫu số ban đầu là (bớt đi 7): 48 - 7 = 41
Tử số ban đầu là (cộng thêm 7): 32 + 7 = 39
ĐS: Phân số cần tìm: 39/41
27 tháng 6 2016
Ta có:
a+6/b+21 = a/b
Nhân chéo ta được: (a + 6)×b = (b + 21)×a
=> ab + 6b = ab + 21a
=> ab - ab = 21a - 6b
=> 3.(7a - 2b) = 0
=> 7a - 2b = 0
=> 7a = 2b
=> a/b = 2/7
Do a/b tối giản nên phân số cần tìm là 2/7
Vậy phân số a/b cần tìm là 2/7
11 tháng 10 2021
Theo đề, ta có:
\(\dfrac{a+31}{a+61}=\dfrac{4}{7}\)
\(\Leftrightarrow7a+217=4a+244\)
hay a=27
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
17 tháng 8 2023
Vì thêm vào tử số 7 đơn vị và giữ nguyên mẫu số thì được phân số có giá trị bằng 1, vậy mẫu số hơn tử số là 7 đơn vị.
Nếu giữ nguyên tử số và cộng thêm vào mẫu số 5 đơn vị thì hiệu mẫu số mới và tử số là:
5 + 7 = 12
Theo bài ra ta có sơ đồ:
theo sơ đồ ta có: Tử số lúc đầu là
12: (3 - 1) = 6
Mẫu số lúc đầu là 6 + 7 = 13
Phân số cần tìm là: \(\dfrac{6}{13}\)
Đs..
Thử lại ta có: \(\dfrac{6+7}{13}\) = 1 (ok)
\(\dfrac{6}{13+5}\) = \(\dfrac{1}{3}\) (ok)
Để câu trả lời của bạn nhanh chóng được duyệt và hiển thị, hãy gửi câu trả lời đầy đủ và không nên: