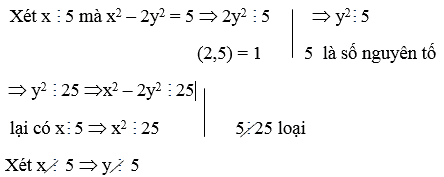Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì 105 là số nguyên lẻ nên 2x+5y+1 và 2020lxl+y+x2+x là số lẻ
=> 5y chẵn => y chẵn
Có:x2+x=x(x+1) là số chẵn nên 2020lxl lẻ
=>x=0
Thay x=0 vào phương trình (2x+5y+1)(2020lxl+y+x2+x)=105 ta được:
\(\left(5y+1\right)\left(y+1\right)=105\Leftrightarrow5y^2+6y-104=0\)
Do \(y\in Z\)nên ta tìm ra y=4
Vậy phương trình có nghiệm là \(\left(x;y\right)=\left(0;4\right)\)

\( (2x+5y+1).(2^{|x|}+y+ x^2 +x)=105\)
Vì 105 là số lẻ nên 2x+5y+1 và 2|x|+y+x2+x cũng là số lẻ.
Có: 2x+5y+1 là số lẻ. Mà 2x+1 là số lẻ
\(\Rightarrow\)5y là số chẵn
\(\Rightarrow\)y là số chắn
Có 2|x|+y+x2+x là só lẻ. Mà x2+x=x(x+1) là tích 2 số tự nhiên liên tiếp nên là số chắn, y cũng là số chẵn
\(\Rightarrow\)2|x| là số lẻ
\(\Rightarrow\)x=0
Thay x=0 vào biểu thức ta có:
\(\left(2.0+5y+1\right)\left(2^{\left|0\right|}+y+0^2+0\right)=105\)
\(\Leftrightarrow\left(0+5y+1\right)\left(1+y+0\right)=105\)
\(\Leftrightarrow\left(5y+1\right)\left(1+y\right)=105\)
\(\Leftrightarrow5y+5y^2+1+y=105\)
\(\Leftrightarrow5y^2+6y+1=105\)
\(\Leftrightarrow5y^2+6y-104=0\)
\(\Leftrightarrow5y^2-20y+26y-104=0\)
\(\Leftrightarrow5y\left(y-4\right)+26\left(y-4\right)=0\)
\(\Leftrightarrow\left(y-4\right)\left(5y+26\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}y-4=0\\5y+26=0\end{cases}\Leftrightarrow\orbr{\begin{cases}y=4\\y=\frac{-26}{5}\end{cases}}}\)
Mà \(x;y\in Z\Rightarrow y=4\)
Vậy x=0;y=4(tmyc)

1: Tìm x, y nguyên tố thoả mãn
y2 – 2x2 = 1
Hướng dẫn:
Ta có y2 – 2x2 = 1 ⇒ y2 = 2x2 +1 ⇒ y là số lẻ
Đặt y = 2k + 1 (với k nguyên).Ta có (2k + 1)2 = 2x2 + 1
⇔ x2 = 2 k2 + 2k ⇒ x chẵn , mà x nguyên tố ⇒ x = 2, y = 3
2: Tìm nghiệm nguyên dương của phương trình
(2x + 5y + 1)(2|x| + y + x2 + x) = 105
Hướng dẫn:
Ta có: (2x + 5y + 1)(2|x| + y + x2 + x) = 105
Ta thấy 105 lẻ ⇒ 2x + 5y + 1 lẻ ⇒ 5y chẵn ⇒ y chẵn
2|x| + y + x2 + x = 2|x| + y + x(x+ 1) lẻ
có x(x+ 1) chẵn, y chẵn ⇒ 2|x| lẻ ⇒ 2|x| = 1 ⇒ x = 0
Thay x = 0 vào phương trình ta được
(5y + 1) ( y + 1) = 105 ⇔ 5y2 + 6y – 104 = 0
⇒ y = 4 hoặc y = ( loại)
Thử lại ta có x = 0; y = 4 là nghiệm của phương trình


16: Tìm nghiệm nguyên của phương trình
x2 –xy + y2 = 3
Hướng dẫn:
Ta có x2 –xy + y2 = 3 ⇔ (x- )2 = 3 –
Ta thấy (x- )2 = 3 –
≥ 0
⇒ -2 ≤ y ≤ 2
⇒ y= ± 2; ±1; 0 thay vào phương trình tìm x
Ta được các nghiệm nguyên của phương trình là :
(x, y) = (-1,-2), (1, 2); (-2, -1); (2,1) ;(-1,1) ;(1, -1)