
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(dat:\frac{x}{2}=\frac{y}{5}=k\)
x=2k ; y=5k
x.y=10k2
10 = 10k2
k2 = 1
k = +-1
Voi : k=1 = > x=1.2=2 ; y=5.1=5
voi : k=-1 => x=-1.2=-2 ; y=-1.5=-5
\(\frac{x}{2}=\frac{y}{3};\frac{y}{4}=\frac{z}{5}\Rightarrow\frac{x}{2}=\frac{4y}{12};\frac{3y}{12}=\frac{z}{5}\Rightarrow\frac{x}{8}=\frac{y}{12};\frac{y}{12}=\frac{z}{15}\Rightarrow\frac{x}{8}=\frac{y}{12}=\frac{z}{15}\)
Ap dung tinh chat day ti so bang nhau ta co :
\(\frac{x}{8}=\frac{y}{12}=\frac{z}{15}=\frac{x+y-z}{8+12-15}=\frac{10}{5}=2\)
Suy ra : \(\frac{x}{8}=2\Rightarrow x=16;\frac{y}{12}=2\Rightarrow y=2.12=24;\frac{z}{15}=2\Rightarrow z=2.15=30\)
nhieu qua lam ko het

2). Ta có: x/2=y/3 => x/8 = y/12
y/4=z/5 => y/12 = z/15
=> x/2=y/12=z/15 và x+y-z=10
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{x}{2}\)=\(\frac{y}{12}\)=\(\frac{z}{15}\)=\(\frac{x+y-z}{2+12-15}\)=\(\frac{10}{-1}\)= -10
=> x=2.(-10)=-20
y=12.(-10)=-120
z=15.(-10)=-150
Vậy x=-20; y=-120;z=-150
3). Đặt \(\frac{x}{2}\)=\(\frac{y}{5}\)= k
=> x=2k
y=5k
Ta có xy = 10
2k.5k =10
10. k2=10
k2 = 10 :10=1
=> k =1; k=-1
+) k = 1
=> x=2.1=2
y=5.1=5
+) k = -1
=> x= 2.(-1) =-2
y=5.(-1) = -5
Vậy x=2;y=5 hoặc x=-2;y=-5
Câu 2:
Ta có \(\frac{x}{2}=\frac{y}{3}=\frac{x}{8}=\frac{y}{12}\)(1)
\(\frac{y}{4}=\frac{z}{5}=\frac{y}{12}=\frac{z}{15}\)(2)
Từ (1) và (2) suy ra:\(\frac{x}{8}=\frac{y}{12}=\frac{z}{15}\)
Áp dụng dãy tỉ số bằng nhau ta có:
\(\Rightarrow\)\(\frac{x}{8}=\frac{y}{12}=\frac{z}{15}=\frac{x+y-z}{8+12-15}=\frac{10}{5}=2\)
\(\Rightarrow\begin{cases}\frac{x}{8}=2\\\frac{y}{12}=2\\\frac{z}{15}=2\end{cases}\)\(\Rightarrow\begin{cases}x=16\\y=24\\z=30\end{cases}\)
Vậy x=16;y=24;z=30

Bài I: Từ \(\frac{x}{2}\)=\(\frac{y}{3}\)\(\Rightarrow\)\(\frac{x}{2}\).\(\frac{1}{4}\)=\(\frac{y}{3}\).\(\frac{1}{4}\)\(\Rightarrow\)\(\frac{x}{8}\)=\(\frac{y}{12}\)(1)
Từ \(\frac{y}{4}\)=\(\frac{z}{5}\)\(\Rightarrow\)\(\frac{y}{4}\).\(\frac{1}{3}\)=\(\frac{z}{5}\).\(\frac{1}{3}\)\(\Rightarrow\)\(\frac{y}{12}\)=\(\frac{z}{15}\)(2)
Từ (1) và (2) suy ra \(\frac{x}{8}\)=\(\frac{y}{12}\)=\(\frac{z}{15}\)
Áp dụng tính chất của dãy tỉ số bằng nhau,ta có:
\(\frac{x}{8}\)=\(\frac{y}{12}\)=\(\frac{z}{15}\)=\(\frac{x+y-z}{8+12-15}\)=\(\frac{10}{5}\)=2
Do đó:\(x=2.8=16\)
\(y=12.2=24\)
\(z=15.2=30\)
Vậy \(x=16\);\(y=24\);\(z=30\)
Bài II: Đặt \(k=\frac{x}{2}\)=\(\frac{y}{5}\)
\(\Rightarrow\)\(x=2.k\);\(y=5.k\)
Vì \(x.y=10\)nên \(2k.5k=10\)
\(\Rightarrow\)\(10.k^2=10\)
\(\Rightarrow\)\(k^2=1\)
\(\Rightarrow\)\(k=1\)hoặc\(k=-1\)
+) Với \(k=1\)thì \(x=2\);\(y=5\)
+) Với \(k=-1\)thì \(x=-2\);\(y=-5\)
Vậy \(x=2\);\(y=5\)hoặc \(x=-2\);\(y=-5\)
\(\frac{x}{2}=\frac{y}{5}\)và \(xy=10\)
Ta có :
\(\frac{x}{2}=\frac{y}{5}\Leftrightarrow5x=2y\Leftrightarrow x=\frac{2y}{5}\). Thay vào biểu thức x . y = 10 . Ta được :
\(\frac{2y}{5}.y=10\Leftrightarrow\frac{2y^2}{5}=10\Leftrightarrow2y^2=50\Leftrightarrow y^2=25\Leftrightarrow y=5;y=-5\)
Với \(y=5\Rightarrow x=\frac{2.5}{5}=2\)
Với \(y=-5\Rightarrow x=\frac{2.\left(-5\right)}{5}=-2\)

\(\frac{x}{2}=\frac{y}{5}=k\rightarrow x=2k;y=5k\)
xy = 10
2k . 5k = 10
10k2 = 10
k2 = 1
k thuộc {-1;2}
k = -1 thì x = -2 ; y = -5
k = 1 thì x = 2 ; y = 5
dat x/2=y/5=5
suy ra: x=2
:y=5
suy ra x .y=2k.5k
xy=10k
ma xy=10k
suy ra 10k2=10
k^2=1
k=1,-1
neu k=1thi x=2,y=5
neu k=-1thi x=-2,y=-5

Đặt x/2=y/5=k
=>x=2k y=5k
Ta có:xy=10
=>2k.5k=10
=>10k2=10
=>k2=1
=>k=1 hoặc k =-1
*)k=1=>x=2k=2 y=5k=5
*)k=-1=>x=2k=-2 y=5k=-5

Ta có : \(\frac{x}{2}=\frac{y}{5}\) =) \(\left(\frac{x}{2}\right)^2=\left(\frac{y}{5}\right)^2\)\(=\frac{x}{2^{ }}.\frac{y}{5^{ }}\)=\(\frac{x.y}{10}=\frac{10}{10}=1\)
=) \(\frac{x^2}{4}=\frac{y^2}{5}=1\)
=) \(x^2=4.1\Rightarrow x=2\) hoặc \(x=-2\)
\(y^2=1.25\Rightarrow x=5\) hoặc \(x=-5\)
Mình chắc chắn đúng đó Kim Ngân!
Đặt x/2 = y/5 = t => x = 2t ; y = 5t
Thay vào ta có x.y= 10 => 2t.5t = 10
=> 10t^2 = 10 => t^2 = 1 => t = 1 hoặc t= - 1
(+) t = 1 => x = 2 ; y = 5
(+) t = -1 => x = -2 ; y = -5

=> x=2k và y=5k
=> x.y=2k.5k=10k2=10
=>k2=1
=>TH1: k=1
=>x=2.1=2 và y=1.5=5
=>TH2: k=-1
=>x=(-1).2=-2 và y=(-1).5=-5
Vậy x=2 thì y=5; x=-2 thì y=-5

Ta có
\(\frac{x}{2}=\frac{y}{5}=k\Rightarrow\hept{\begin{cases}x=2k\\y=5k\end{cases}}\)
\(\Rightarrow x\cdot y=2k\cdot5k=10\)
\(\Rightarrow k^2\cdot10=10\)
\(\Rightarrow k^2=1\)
\(\Rightarrow k^2=1^2\)
\(\Rightarrow k=1\)
Thay K=1 vào x;y ta có
\(\hept{\begin{cases}x=2k=2\\y=5k=5\end{cases}}\)
ti ck nha
\(\frac{x}{2}=\frac{y}{5}\Rightarrow\left(\frac{x}{2}\right)^2=\left(\frac{y}{5}\right)^2=\frac{x}{2}.\frac{y}{5}=\frac{x.y}{2.5}=\frac{10}{10}=1\)
\(\Rightarrow\hept{\begin{cases}x=2.1=2\\y=5.1=5\end{cases}}\)
Vậy x = 2, y = 5
P/s: Cô mình có dạy tính chất a = b => a2 = b2 = ab nên mình áp dụng theo

Đặt k =  . Ta có x = 2k, y = 5k
. Ta có x = 2k, y = 5k
Từ xy=10. suy ra 2k.5k = 10 => 10 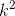 = 10 =>
= 10 => 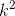 = 1 => k = ± 1
= 1 => k = ± 1
Với k = 1 ta được  = 1 suy ra x = 2, y = 5
= 1 suy ra x = 2, y = 5
Với k = -1 ta được  = -1 suy ra x = -2, y = -5
= -1 suy ra x = -2, y = -5
Gọi \(\dfrac{x}{2}=\dfrac{y}{5}=k\)
Với \(\dfrac{x}{2}=k\Rightarrow x=2k\); \(\dfrac{y}{5}=k\Rightarrow y=5k\)
Theo đề bài,ta còn có:
\(xy=10\)
hay 2k.5k=10
10k2 =10
\(\Rightarrow k=\pm1\)
Với k=1 \(\Rightarrow\dfrac{x}{2}=\dfrac{y}{5}=1\Rightarrow x=2;y=5\)
Với k=-1 \(\Rightarrow\dfrac{x}{2}=\dfrac{y}{5}=-1\Rightarrow x=-2;y=-5\)
=> x = 2k và y = 5k
Từ xy = 10 suy ra
2k.5k = 10 => 10k2 = 10 => k = ±1
- Với k = 1 ta được x = 2; y = 5
Toán 7 hả ?
Đặt \(\frac{x}{2}=\frac{y}{5}=k\)
\(\Rightarrow\hept{\begin{cases}x=2k\\y=5k\end{cases}}\)
Theo bài ra ta có:
xy=2k.5k=10
=> 10k2=10
=> k=\(\pm\)1
Với k = 1 suy ra
\(\hept{\begin{cases}x=2\\y=5\end{cases}}\)
Với k = -1 suy ra
\(\hept{\begin{cases}x=-2\\y=-5\end{cases}}\)
Đáp số: ...