K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
22 tháng 12 2020
Lời giải:
\(y=-4\cos ^2x+2\sin x+3=-4(1-\sin ^2x)+2\sin x+3=4\sin ^2x+2\sin x-1\)
Đặt \(\sin x=t(t\in [-1;1])\) thì:
\(y=4t^2+2t-1\)
\(y'=8t+2=0\Leftrightarrow t=-\frac{1}{4}\)
Lập BBT. Với các giá trị \(y(\frac{-1}{4})=\frac{-5}{4}; y(-1)=1; y(1)=5\) ta thấy:
\(y_{\max}=5\Leftrightarrow t=1\Leftrightarrow x=2k\pi +\frac{\pi}{2}\)
\(y_{\min}=\frac{-5}{4}\Leftrightarrow t=\frac{-1}{4}\Leftrightarrow x=2k\pi -2\tan ^{-1}(4\pm \sqrt{15})\)
DG
1
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 9 2021
Đặt \(\left\{{}\begin{matrix}\sqrt{5sin^2x+1}=a\\\sqrt{5cos^2x+1}=b\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}1\le a;b\le\sqrt{6}\\a^2+b^2=5\left(sin^2x+cos^2x\right)+2=7\end{matrix}\right.\)
\(y=a+b\le\sqrt{2\left(a^2+b^2\right)}=\sqrt{14}\)
\(y_{max}=\sqrt{14}\) khi \(cos2x=0\Rightarrow x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
Do \(1\le a\le\sqrt{6}\Rightarrow\left(a-1\right)\left(a-\sqrt{6}\right)\le0\)
\(\Rightarrow a\ge\dfrac{a^2+\sqrt[]{6}}{\sqrt{6}+1}\)
Tương tự ta có \(b\ge\dfrac{b^2+\sqrt{6}}{\sqrt{6}+1}\)
\(\Rightarrow y=a+b\ge\dfrac{a^2+b^2+2\sqrt{6}}{\sqrt{6}+1}=\dfrac{7+2\sqrt{6}}{\sqrt{6}+1}=\sqrt{6}+1\)
\(y_{min}=\sqrt{6}+1\) khi \(sin2x=0\Rightarrow x=\dfrac{k\pi}{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 7 2021
\(y=\left|2sin^2x-sinx-1\right|-2sinx\)
Đặt \(sinx=t\in\left[-1;1\right]\)
\(\Rightarrow y=f\left(t\right)=\left|2t^2-t-1\right|-2t\)
BBT cho \(f\left(t\right)\) trên \(\left[-1;1\right]\):
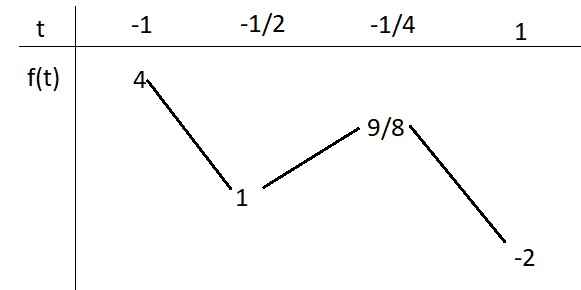
Từ BBT ta thấy \(y_{max}=4\) khi \(sinx=-1\); \(y_{min}=-2\) khi \(sinx=1\)
T
1 tháng 8 2018
1. Do \(\cos x+2>0\forall x\in R\) \(\Rightarrow\) Hàm số xác định \(\forall x\in R\)
\(y=\dfrac{\sin x+1}{\cos x+2}\)
\(\Leftrightarrow\)\(y\cos x-\sin x=1-2y\)
pt có nghiệm \(\Leftrightarrow y^2+\left(-1\right)^2\ge\left(1-2y\right)^2\)
\(\Leftrightarrow3y^2-4y\le0\)
\(\Leftrightarrow0\le y\le\dfrac{4}{3}\)
2. \(y=\dfrac{\cos x+2\sin x+3}{2\cos x-\sin x+4}\)
\(\Leftrightarrow\left(2y-1\right)\cos x-\left(y+2\right)\sin x=3-4y\)
pt có nghiệm \(\Leftrightarrow\left(2y-1\right)^2+\left(y+2\right)^2\ge\left(3-4y\right)^2\)
\(\Leftrightarrow11y^2-24y+4\le0\)
\(\Leftrightarrow\dfrac{2}{11}\le y\le2\)
kiểm tra giúp mình xem có sai sót gì không...
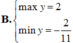
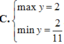
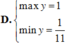
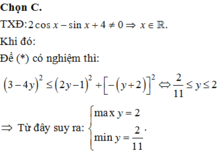
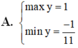
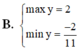
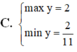
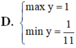
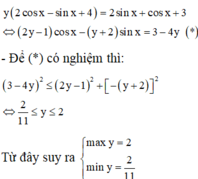
\(y=-5\left(1-sin^2x\right)+2sinx+8=5sin^2x+2sinx+3\)
\(y=5\left(sinx+\frac{1}{5}\right)^2+\frac{14}{5}\ge\frac{14}{5}\)
\(y_{min}=\frac{14}{5}\) khi \(sinx=-\frac{1}{5}\)
\(y=\left(5sinx+7\right)\left(sinx-1\right)+10\le10\)
\(y_{max}=10\) khi \(sinx=1\)
Dạ nếu bài này xét trên đoạn \(\left[\dfrac{-\pi}{6};\dfrac{5\pi}{6}\right]\) thì nó có ra kết quả vậy không a :v Em làm ra kết quả như a làm ấy mà sao Min nó xấu quá. Em cảm ơn!