
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a2 - 2a + 6b + b2 = -10
<=> a2 - 2a + 6b + b2 + 10 = 0
<=> ( a2 - 2a + 1 ) + ( b2 + 6b + 9 ) = 0
<=> ( a - 1 )2 + ( b + 3 )2 = 0 (*)
\(\hept{\begin{cases}\left(a-1\right)^2\ge0\forall a\\\left(b+3\right)^2\ge0\forall b\end{cases}}\Rightarrow\left(a-1\right)^2+\left(b+3\right)^2\ge0\forall a,b\)
Đẳng thức xảy ra ( tức (*) ) <=> \(\hept{\begin{cases}a-1=0\\b+3=0\end{cases}}\Rightarrow\hept{\begin{cases}a=1\\b=-3\end{cases}}\)
Vậy a = 1 ; b = -3


\(a.\)
Phân tích biển đổi thành nhân tử kết hợp với chuyển vế để quy về hẳng đẳng thức, khi đó, ta tính được \(a,b\)
Thật vậy, ta có:
\(a^2-2a+6b+b^2=-10\)
\(\Leftrightarrow\) \(a^2-2a+6b+b^2+10=0\)
\(\Leftrightarrow\) \(\left(a^2-2a+1\right)+\left(b^2+6b+9\right)=0\)
\(\Leftrightarrow\) \(\left(a-1\right)^2+\left(b+3\right)^2=0\) \(\left(1\right)\)
Vì \(\left(a-1\right)^2\ge0;\) \(\left(b+3\right)^2\ge0\) với mọi \(a,b\)
nên để thỏa mãn đẳng thức \(\left(1\right)\) thì phải xảy ra đồng thời \(\left(a-1\right)^2=0\) và \(\left(b+3\right)^2=0\)
\(\Leftrightarrow\) \(a-1=0\) và \(b+3=0\) \(\Leftrightarrow\) \(a=1\) và \(b=-3\)
\(b.\) Cộng \(1\) vào mỗi phân thức của biểu thức \(A\), khi đó, ta có:
\(A+3=\left(\frac{x+y}{z}+1\right)+\left(\frac{x+z}{y}+1\right)+\left(\frac{y+z}{x}+1\right)=\frac{x+y+z}{z}+\frac{x+y+z}{y}+\frac{x+y+z}{x}\)
\(A+3=\left(x+y+z\right)\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)=0\) (do \(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=0\))
Vậy, \(A=-3\)

a) \(a^2+b^2+1\ge ab+a+b\Leftrightarrow2a^2+2b^2+2\ge2ab+2a+2b\)
\(\Leftrightarrow\left(a^2-2ab+b^2\right)+\left(a^2-2a+1\right)+\left(b^2-2b+1\right)\ge0\)
\(\Leftrightarrow\left(a-b\right)^2+\left(a-1\right)^2+\left(b-1\right)^2\ge0\) (luôn đúng)
Dấu "=" xảy ra <=> a=b=1.
b) \(a^2-2a+6b+b^2=-10\Leftrightarrow\left(a^2-2a+1\right)+\left(b^2+6b+9\right)=0\)
\(\Leftrightarrow\left(a-1\right)^2+\left(b+3\right)^2=0\). Mà \(\left(a-1\right)^2\ge0;\left(b+3\right)^2\ge0\forall a;b\)
Nên \(\hept{\begin{cases}\left(a-1\right)^2=0\\\left(b+3\right)^2=0\end{cases}\Leftrightarrow\hept{\begin{cases}a=1\\b=-3\end{cases}}}\). KL: ...

\(a^2-6a+6b+b^2=-10\)
\(\Leftrightarrow a^2-2a+6b+b^2+10=0\)
\(\Leftrightarrow\left(a^2-2a+1\right)+\left(b^2+6b+9\right)=0\)
\(\Leftrightarrow\left(a^2-2.a.1+1^2\right)+\left(b^2+2.b.3+3^2\right)=0\)
\(\Leftrightarrow\left(a-1\right)^2+\left(b+3\right)^2=0\) (1)
Vì \(\left(a-1\right)^2+\left(b+3\right)^2\ge0\) với mọi a;b
Nên để thỏa mãn (1) thì \(\left(a-1\right)^2=\left(b+3\right)^2=0\Leftrightarrow a=1;b=-3\)

a2 - 2a + 6b + b2 = - 10
=> ( a2 - 2a + 1 ) + ( b2 + 6b + 9 ) = 0
=> ( a - 1 )2 + ( b + 3 )2 = 0
Mà ( a - 1 )2 \(\ge\) 0; ( b + 3 )2 \(\ge\)0
Dấu "=" xảy ra khi :
\(\left\{{}\begin{matrix}a-1=0\\b+3=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=1\\b=-3\end{matrix}\right.\)

a) Ta có: \(a^2-2a+2\)
\(=\left(a^2-2a+1\right)+1\)
\(=\left(a-1\right)^2+1>0\) với mọi a
\(=>\left(đpcm\right)\)
b)Ta có: \(6b-b^2-10\)
\(=-\left(b^2-6b+3^2\right)-1\)
\(=-\left(b-3\right)^2-1< 0\) với mọi b
=>(đpcm).
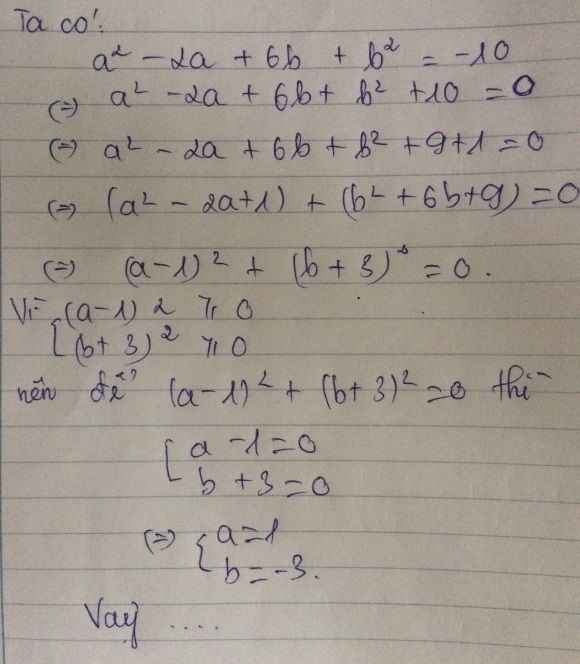
\(\Leftrightarrow a^2-2a+1+b^2+6b+9=0\)
\(\Leftrightarrow\left(a-1\right)^2+\left(b+3\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}a-1=0\\b+3=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=-3\end{matrix}\right.\)