NT
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TS
1
26 tháng 5 2015
\(3^{2015}=3^{4.503+3}=\left(3^4\right)^{503}.27=\left(...1\right).27=\left(...7\right)\)
\(7^{2016}=\left(7^4\right)^{504}=\left(...1\right)^{504}=\left(...1\right)\)
\(9^{2017}=\left(9^2\right)^{1008}.9=\left(...1\right).9=\left(...9\right)\)
\(19^{2015}=\left(19^2\right)^{1007}.19=\left(...1\right)^{1007}.19=\left(...1\right).19=\left(...9\right)\)
=> 32015.72016.92017.192015 = \(\left(...7\right).\left(...1\right).\left(...9\right).\left(...9\right)=\left(...7\right)\)
PN
1
JK
27 tháng 9 2019
\(7^{1999}=7^{1996}\cdot7^3=\overline{......1}\cdot\overline{......3}=\overline{......3}\)
\(8^{2015}=8^{2012}\cdot8^3=\overline{.....6}\cdot\overline{......2}=\overline{......2}\)
\(9^{3^2}=9^9=9^8\cdot9=\overline{......1}\cdot\overline{......9}=\overline{.....9}\)
\(87^{32}=\overline{......1}\)
\(58^{33}=58^{32}\cdot58=\overline{.....6}\cdot58=\overline{.....8}\)
PN
3
22 tháng 4 2016
Những số có tận cùng là 5 thì mũ bao nhiêu cũng vẫn sẽ có tận cùng là 5 và nó có dạng:\(...5^x=...5\)
Vậy 2015^2016= một số có tận cùng là 5
Những số có tận cùng là 4 mà số mũ của nó là số lẻ thì nó sẽ có số tận cùng là 4 và nó có dạng:\(...4^x=...4\)
Vì 2015^2016 là số lẻ nên 2014^2015^2016 sẽ có số tận cùng là 4
cho minh nha
PT
0
LT
0
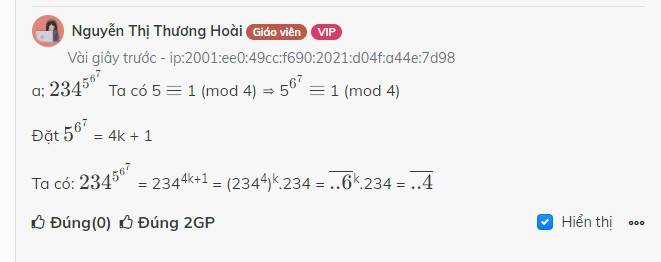
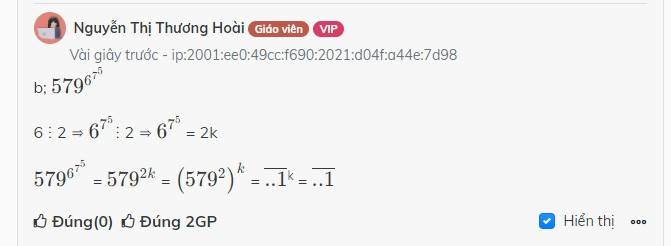
a) Nhân thấy : 1000 = 4k
Nên 21000 = 24k = ...6k
Vì ...6k có tận cùng là 6 nên 21000 có tận cùng là 6
b) Nhận thấy 2015 = 2k + 1
Nên 192015 = 192k+1 = 192k.19 = ...1k .19
Vì ...1k có tận cùng là 1 nên 192015 có tận cùng là 9
c) Nhận thấy 2016 = 4k
Nên 72016 = 74k = ...1k
Vì ...1k có tận cùng là 1 nên 72016 có tận cùng là 1
Do 72016 có tận cùng là 1 nên 72016 lũy thừa lên \(7^{2016^{2017}}\) vẫn có tận cùng là 1