Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

các phấn số trên là số nguyên thì tử phải chia hết cho mẫu
suy ra mẫu là ước của tử
các câu đều chung 1 dạng như vậy đó
tự làm tiếp nha tui đi ngủ đây
a) n+4/n
=n/n+4/n
=1+4/n
Để 1+4/n là số nguyên
=> 4/n là số nguyên và n là số tự nhiên
=> n là Ư(4) =1;2;4
b,c áp dụng tương tự câu a
d) thì khó hơn xíu mik giải hộ:
n/n-2 là số nguyên
=> D=n/n-2
=> 2D=2n/n-2
=> 2D=2n-4+4/n-2
=> 4/n-2 là số nguyên do 2n-4=2(n-2) chia hết cho n-2
=> n-2 là Ư(4)
Xong tự giải típ .
Cho phân số \(A=\dfrac{6}{n-3}\) với n là số tự nhiên. Phân số A bằng bao nhiêu nếu \(n=14;n=5;n=3\)

Nếu n = 14 thì A = 6/11
Nếu n = 5 thì A = 6/2
Nếu n = 3 thì A =6/1

b)
\(B=\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2016}}\\ 2B=1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2015}}\\ 2B-B=\left(1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2015}}\right)-\left(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2016}}\right)\\ B=1-\dfrac{1}{2^{2016}}< 1\)
Vậy B < 1 (đpcm)

a)Vì n chia hết cho n nên để n+4 chia hết cho n thì n thuộc Ư(4).Mà Ư(4)=1;2;4.Vậy n=1;2;4

\(\frac{2n+7}{n-1}=2+\frac{9}{n-1}\)
Để \(2+\frac{9}{n-1}\)có giá trị là số tự nhiên thì n-1 là ước của 9 và ước tự nhiên
=> Ư(9)={1;3;9}
Với n-1=1=> n=2 (TM)
n-1=3=> n=4 (TM)
n-1=9=> n=10 TM)
Vậy n ={2;4;10} để \(\frac{2n+7}{n-1}\)có giá trị là số tự nhiên

Ta có : \(\frac{n+3}{n-3}=\frac{n-3+6}{n-3}=\frac{n-3}{n-3}+\frac{6}{n-3}=1+\frac{6}{n-3}\)( có giá trị là số tự nhiên )
Mà \(1\in N\Leftrightarrow\frac{6}{n-3}\in N\)
\(\Leftrightarrow\left(n-3\right)\inƯ_6=\left\{1;2;3;6\right\}\)
\(\Rightarrow n=\left\{4;5;6;9\right\}\)
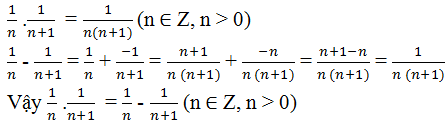

(làm câu dễ nhất...> . < ...)
c)Để \(\dfrac{6}{n-1}\) là số nguyên thì 6 ⋮ \(n-1\)
\(\Rightarrow n-1\inƯ\left(6\right)=\left\{\pm1,\pm2,\pm3,\pm6\right\}\)
Ta có bảng sau :
n-1 n -1 -2 -3 -6 1 2 3 6 0 -1 -2 -5 2 3 4 7
Vậy để \(\dfrac{6}{n-1}\) là số nguyên thì \(x=\left\{0;-1;-2;-5;2;3;4;7\right\}\)
d) \(\dfrac{n}{n-2}=\dfrac{n-2+2}{n-2}\) là số nguyên thì \(n-2+2⋮n-2\Rightarrow2⋮n-2\Rightarrow n-2\inƯ\left(2\right)=\left\{\pm1;\pm2\right\}\)
Ta có bảng sau:
n-2 n -1 -2 1 2 1 3 0 4 Vậy với \(x=\left\{1;3;0;4\right\}\) thì \(\dfrac{n}{n-2}\) là số nguyên
(chắc sai... > . < ...)