ND
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
10 tháng 9 2020
BÀI GIẢI
VÌ A là số tự nhiên chia hết cho 9 nên tổng các chữ số của A phải chia hết cho 9 suy ra số A có dạng đơn giản nhất là 1000...08 (với chữ số 0 xuất hiện 2018 lần)
B là tổng các chữ số của A nên +
C là tổng các chữ số của B nên
D là tổng các chữ số của C nên
đáp án là 9
AH
Akai Haruma
Giáo viên
4 tháng 3 2017
Lời giải:
Vì mặt phẳng đi qua $A$ nên có dạng
\((P):a(x-1)+b(y-2)+c(z-3)=0\)
Ta có \(\overrightarrow{AB}=(-3,-1,2)\). Vì PT mặt phẳng đi qua $A,B$ nên
\(\overrightarrow{n_P}=(a,b,c)\perp \overrightarrow{AB}\Rightarrow -3a-b+2c=0\) \((1)\)
\(d(C,(P))=2d(D,(P))\Leftrightarrow \frac{|a-3b-2c|}{\sqrt{a^2+b^2+c^2}}=\frac{2|-a+b-2c|}{\sqrt{a^2+b^2+c^2}}\)
\(\Leftrightarrow (a-3b-2c)^2=4(-a+b-2c)^2\) \((2)\)
Từ \((1)\) thay \(2c=3a+b\) vào \((2)\) và khai triển thu được: \(\left[{}\begin{matrix}b=\dfrac{3a}{2}\\b=\dfrac{-5a}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}c=\dfrac{9a}{4}\\c=\dfrac{a}{4}\end{matrix}\right.\)
Do đó PTMP \(\left[{}\begin{matrix}a\left(x-1\right)+\dfrac{3}{2}a\left(y-2\right)+\dfrac{9}{4}a\left(z-3\right)=0\\a\left(x-1\right)-\dfrac{5}{2}a\left(y-2\right)+\dfrac{1}{4}a\left(z-3\right)=0\end{matrix}\right.\)
\(\leftrightarrow\left[{}\begin{matrix}4x+6y+9z-43=0\\4x-10y+z+13=0\end{matrix}\right.\)
14 tháng 12 2016
ta có BI=\( \frac{2a}{3}\).nhận thấy góc giữa hai mp(B\(B^,C^,C\)) và đáy là góc giữa hai đường thẳng \(BB^,\) vàAB =30\(^o \)
Xét tam giác \(BB^,I\) vông tại I có:
tan(30)=\(\frac{B^, I}{IB}\)=\(\frac{h}{\frac{2a}{3}}\) →h=\(\frac{2\sqrt{3}a}{9}\) từ đó suy ra thể tích V=h.S=\(\frac{2\sqrt{3}a^3}{9}\)
CM
17 tháng 4 2019
Chọn A
Cách 1: Ta có
Do ABCD là hình thang cân nên
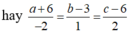
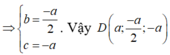
Lại có AC = BD
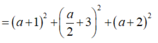
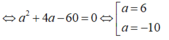
Với a = -10 => D(-10;5;10). Kiểm tra thấy: A B → = C D → (Không thỏa mãn ABCD là hình thang cân).
Với a= 6 => D(6; -3; -6). Kiểm tra thấy: 3. A B → = C D → ( thỏa mãn).
Do đó
Cách 2
Ta có
Do ABCD là hình thang cân nên A B → ; C D → ngược hướng hay
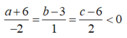
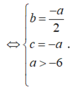
Lại có AB = CD
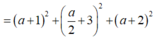
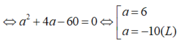
Do đó
Cách 3
+ Viết phương trình mặt phẳng trung trực của đoạn thẳng AB( cũng là mp trung trực của đoạn thẳng CD )
+ Gọi mp α là mặt phẳng trung trực của đoạn thẳng AB, suy ra mp α đi qua trung điểm I(1;2;0) của đoạn thẳng AB và có một vectơ pháp tuyến là
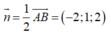
suy ra phương trình của mp α là :
+ Vì C, D đối xứng nhau qua mp α nên
Công thức trắc nghiệm
Xác định toạ độ điểm M ' ( x 1 ; y 1 ; z 1 ) là điểm đối xứng của điểm M ( x 0 ; y 0 ; z 0 ) qua mp
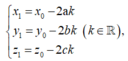
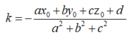
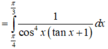
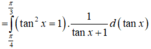
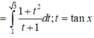
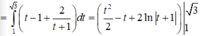
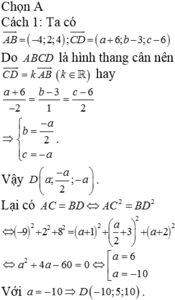
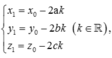
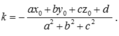
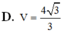
ta gọi số cần tìm có dạng abcd và tổng các chữ số là (a+b+c+d). ĐK: a,b,c,d thuộc (0;10)
vì 0<(a+b+c+d)<40
<=> 2359 - 0 < 2359 - (a+b+c+d) < 2359 - 4
mặt khác, vì abcd + (a+b+c+d) = 2359 => abcd = 2359 - (a+b+c+d)
thay vào, ta có:
2359 > abcd > 2319
số abcd nằm trong khoảng (2319->2359) => số đó phải có dạng 23xy => a=2,b=3, cd thuộc khoảng (19->59)
mà ta có abcd + (a+b+c+d) = 2359
<=> 2300 + cd + (2+3+c+d) = 2359
<=> 11c + 2d = 54
<=> d = (54-11c)/2
để d là số tự nhiên => (54-11c) phải là số chẵn => c phải chẵn
c= 0 => d=54/2 = 27 (>9) => loại
c= 2 => d= 32/2 = 16 (>9) => loại
c= 4 => d= 10/2 = 5
=> số cần tìm abcd chính là 2345
2345 NHA
HT
chúc bn năm mới vui vẻ
@@@@@@@@@@@@@@@@@@@