Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: \(6x=4y=3z\Rightarrow\dfrac{6x}{12}=\dfrac{4y}{12}=\dfrac{3z}{12}\Rightarrow\dfrac{x}{2}=\dfrac{2y}{6}=\dfrac{3z}{12}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{2}=\dfrac{2y}{6}=\dfrac{3z}{12}=\dfrac{x+2y-3z}{2+6-12}=\dfrac{-2}{-4}=\dfrac{1}{2}.\)
Với: \(\dfrac{x}{2}=\dfrac{1}{2}\Rightarrow x=1.\)
\(\dfrac{2y}{6}=\dfrac{y}{3}=\dfrac{1}{2}\Rightarrow y=\dfrac{1}{2}.3=\dfrac{3}{2}.\)
\(\dfrac{3z}{12}=\dfrac{z}{4}=\dfrac{1}{2}\Rightarrow z=\dfrac{1}{2}.4=\dfrac{4}{2}=2.\)
Vậy: \(x=1;y=\dfrac{3}{2};z=2.\)

Theo đề : \(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}\) và \(x^2+y^2+2z^2=108\)
\(\Rightarrow\left(\dfrac{x}{2}\right)^2=\left(\dfrac{y}{3}\right)^2=\left(\dfrac{z}{4}\right)^2\Rightarrow\left(\dfrac{x}{2}\right)^2=\left(\dfrac{y}{3}\right)^2=2.\left(\dfrac{z}{4}\right)^2=>\dfrac{x^2}{4}=\dfrac{y^2}{9}=\dfrac{2z^2}{32}\)
Áp dụng t/c dãy tỉ số bằng nhau:
\(\dfrac{x^2}{4}=\dfrac{y^2}{9}=\dfrac{2z^2}{32}=\dfrac{x^2+y^2+2z^2}{4+9+32}=\dfrac{108}{45}=\dfrac{12}{5}\)
Với \(\dfrac{x^2}{2}=\dfrac{12}{5}\Rightarrow x^2=\dfrac{12}{5}.2=\dfrac{24}{5}\Rightarrow x=\dfrac{2\sqrt{30}}{5}\)
\(\dfrac{y^2}{3}=\dfrac{12}{5}\Rightarrow y^2=\dfrac{12}{5}.3=\dfrac{36}{5}\Rightarrow y=\dfrac{6\sqrt{5}}{5}\)
\(\dfrac{2z^2}{4}=\dfrac{12}{5}\Rightarrow2z^2=\dfrac{12}{5}.4=\dfrac{48}{5}\Rightarrow z^2=\dfrac{24}{5}=>\dfrac{2\sqrt{30}}{5}\)

theo bài ra ta có:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}\)
dựa vào tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}\\ =\dfrac{x^2}{4}=\dfrac{y^2}{9}=\dfrac{2z^2}{32}\\ =\dfrac{x^2-y^2+2z^2}{4-9+32}=\dfrac{108}{27}=4\)=>x=4.2=8
=>y=4.3=12 =>z=4.4=16 vậy x,y,z lần lượt là 8;12;16

Sửa đề: \(x^2-y^2+2z^2=108\)
Đặt x/2=y/3=z/5=k
=>x=2k; y=3k; z=5k
Ta có: \(x^2-y^2+2z^2=108\)
\(\Leftrightarrow4k^2-9k^2+50k^2=108\)
=>45k2=108
=>k2=12/5
TH1: \(k=\dfrac{2\sqrt{3}}{\sqrt{5}}\)
=>\(x=\dfrac{4\sqrt{3}}{\sqrt{5}};y=\dfrac{6\sqrt{3}}{\sqrt{5}};z=2\sqrt{15}\)
TH2: \(k=-\dfrac{2\sqrt{3}}{\sqrt{5}}\)
=>\(x=-\dfrac{4\sqrt{3}}{\sqrt{5}};y=-\dfrac{6\sqrt{3}}{\sqrt{5}};z=-2\sqrt{15}\)

a, \(\frac{2}{3}x=\frac{3}{4}y=\frac{4}{5}z\)
\(\Rightarrow\frac{2x}{3.12}=\frac{3y}{4.12}=\frac{4z}{5.12}\)
\(\Rightarrow\frac{x}{18}=\frac{y}{16}=\frac{z}{15}=\frac{x+y+z}{18+16+15}=\frac{45}{49}\)
Đến đây tự làm tiếp nhé
b, \(2x=3y=5z\Rightarrow\frac{2x}{30}=\frac{3y}{30}=\frac{5z}{30}\Rightarrow\frac{x}{15}=\frac{y}{10}=\frac{z}{6}=\frac{x+y-z}{15+10-6}=\frac{95}{19}=5\)
=> x = 75, y = 50, z = 30
c, \(\frac{3}{4}x=\frac{5}{7}y=\frac{10}{11}z\)
\(\Rightarrow\frac{3x}{4.30}=\frac{5y}{7.30}=\frac{10z}{11.30}\)
\(\Rightarrow\frac{x}{40}=\frac{y}{42}=\frac{z}{33}\)
\(\Rightarrow\frac{2x}{80}=\frac{3y}{126}=\frac{4z}{132}=\frac{2x-3y+4z}{80-126+132}=\frac{8,6}{86}=\frac{1}{10}\)
=> x=... , y=... , z=...
d, Đặt \(\frac{x}{2}=\frac{y}{5}=k\Rightarrow x=2k,y=5k\)
Ta có: xy = 90 => 2k.5k = 90 => 10k2 = 90 => k2 = 9 => k = 3 hoặc -3
Với k = 3 => x = 6, y = 15
Với k = -3 => x = -6, y = -15
Vậy...
e, Tương tự câu d
b) Ta có :\(\text{ 2x = 3y = 5z }=\frac{x}{\frac{1}{2}}=\frac{y}{\frac{1}{3}}=\frac{z}{\frac{1}{5}}=\frac{x+y-z}{\frac{1}{2}+\frac{1}{3}-\frac{1}{5}}=\frac{95}{\frac{19}{30}}=\frac{1}{6}\)
=> \(2x=\frac{1}{6}\Rightarrow x=\frac{1}{12}\)
\(3y=\frac{1}{6}\Rightarrow y=\frac{1}{18}\)
\(5z=\frac{1}{6}\Rightarrow z=\frac{1}{30}\)

a) \(\dfrac{x}{2}=\dfrac{y}{3};\dfrac{y}{5}=\dfrac{z}{4}\) và \(x-y+z=-49\)
Ta có:
\(\dfrac{x}{2}=\dfrac{y}{3}\Rightarrow\dfrac{x}{10}=\dfrac{y}{15}\) (1)
\(\dfrac{y}{5}=\dfrac{z}{4}\Rightarrow\dfrac{y}{15}=\dfrac{z}{12}\) (2)
Từ (1) và (2) suy ra \(\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{12}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{12}=\dfrac{x-y+z}{10-15+12}=\dfrac{-49}{7}=-7\)
Vậy \(\left\{{}\begin{matrix}x=\left(-7\right).10=-70\\y=\left(-7\right).15=-105\\z=\left(-7\right).12=-84\end{matrix}\right.\)
b) \(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}\) và \(x^2-y^2+2z^2=10\)
Ta có: \(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}\Rightarrow\dfrac{x^2}{4}=\dfrac{y^2}{9}=\dfrac{2z^2}{32}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{x^2}{4}=\dfrac{y^2}{9}=\dfrac{2z^2}{32}=\dfrac{x^2-y^2+2z^2}{4-9+32}=\dfrac{10}{27}\)
Vậy ... (tự tính x, y, z nhé!)

Ta có:
\(\left\{{}\begin{matrix}x^2+xy+\dfrac{y^2}{3}=2019\\z^2+\dfrac{y^2}{3}=1011\\x^2+xz+z^2=1008\end{matrix}\right.\Leftrightarrow x^2+xy+\dfrac{y^2}{3}=z^2+\dfrac{y^2}{3}+x^2+xz+z^2\)
\(\Rightarrow xy=2z^2+xz\Leftrightarrow xy+xz=2z^2+2xz\)
\(\Rightarrow x\left(y+z\right)=2z\left(x+z\right)\Leftrightarrow\dfrac{2z}{x}=\dfrac{y+z}{x+z}\left(đpcm\right)\)

Ta có: \(\dfrac{x}{2}=\dfrac{x^2}{4}\) ; \(\dfrac{y}{3}=\dfrac{y^2}{9}\) ; \(\dfrac{z}{4}=\dfrac{2z^4}{32}\)
Ta có: \(\dfrac{x^2}{4}=\dfrac{y^2}{9}=\dfrac{2z^2}{32}=\dfrac{x^2-y^2+2z^2}{4-9+32}=\dfrac{108}{27}=4\)
\(x=4.2=8\)
\(y=4.3=12\)
\(z=4.32=128\)
Vậy 3 số cần tìm là:
x = 8; y = 12; z=128

Ta có \(\dfrac{x}{2}=\dfrac{y}{3}\Rightarrow\dfrac{x}{2.4}=\dfrac{y}{3.4}\Rightarrow\dfrac{x}{8}=\dfrac{y}{12}\)
\(\dfrac{y}{4}=\dfrac{z}{5}\Rightarrow\dfrac{y}{4.3}=\dfrac{z}{3.5}\Rightarrow\dfrac{y}{12}=\dfrac{z}{15}\)
Do đó \(\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{z}{15}và\) \(x+y-z=10\)
Áp dụng tính chất của dãy tỉ số bằng nhau,ta được:
\(\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{z}{15}=\dfrac{x+y-z}{8+12-15}=\dfrac{10}{5}=2\)
Với\(\dfrac{x}{8}=2\Rightarrow x=16\)
\(\dfrac{y}{12}=2\Rightarrow y=24\)
\(\dfrac{z}{15}=2\Rightarrow z=30\)
Vậy x=16, y=24 và z=30
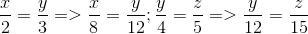
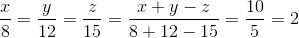
Ta có: x/2=y/3=z/4→x2/4=y2/9=2x2/32=x2-y2+2z2/4-9+32=108/27=81
Với x/2=81→x=81.2=162
Với y/3=81→y=81.3=243
Với z/4=81→81.4=324
Ta có:\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}\Rightarrow\dfrac{x^2}{4}=\dfrac{y^2}{9}=\dfrac{z^2}{16}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ,ta có:
\(\dfrac{x^2}{4}=\dfrac{y^2}{9}=\dfrac{z^2}{16}=\dfrac{2z^2}{32}=\dfrac{x^2-y^2+2z^2}{4-9+32}=\dfrac{108}{27}=4\)
\(\dfrac{x^2}{4}=4\Rightarrow x^2=16\Rightarrow x=4\)
\(\dfrac{y^2}{9}=4\Rightarrow y^2=36\Rightarrow y=6\)
\(\dfrac{z^2}{16}=4\Rightarrow z^2=64\Rightarrow z=8\)