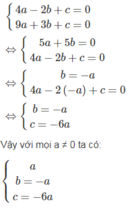Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để 2 pt có nghiệm \(\hept{\begin{cases}\Delta_1=b^2-4.1102.2011\ge0\\\Delta_2=b^2-4.2011.1102\ge0\end{cases}}\Leftrightarrow b^2\ge4.2011.1102\Leftrightarrow\orbr{\begin{cases}b\ge2\sqrt{2011.1102}\\b\le-2\sqrt{2011.1102}\end{cases}}\)
Giả sử x0 là nghiệm chung của 2 pt (1) và (2) \(\Rightarrow\)\(\hept{\begin{cases}2011x_0^2+bx_0+1102=0\left(3\right)\\1102x_0^2+bx_0+2011=0\left(4\right)\end{cases}}\)
trừ theo vế 2 pt (3) và (3) ta được: \(909x_0^2-909=0\)\(\Leftrightarrow\)\(x_0^2=1\)\(\Leftrightarrow\)\(\orbr{\begin{cases}x_0=1\\x_0=-1\end{cases}}\)
+) Với x0=1, thay vào pt (3) ta đc: \(2011+b+1102=0\)\(\Leftrightarrow\)\(b=-3113\left(tm\right)\)
+) Với x0=-1, thay vào pt (3) ta đc: \(1102-b+2011=0\)\(\Leftrightarrow\)\(b=3113\left(tm\right)\)
...

Gọi nghiệm chung của 2 phương trình là m
Ta có:\(m^2+am+1=0;m^2+bm+17=0\)
\(\Rightarrow2m^2+m\left(a+b\right)+18=0\)
Xét \(\Delta=\left(a+b\right)^2-144\ge0\Rightarrow\left|a+b\right|\ge12\)
Mà \(\left|a\right|+\left|b\right|\ge\left|a+b\right|\ge12\)
Xét \(a+b=12\Rightarrow.....\)
Xét \(a+b=-12\Rightarrow....\)
Mấy chỗ ..... bạn tự làm nốt

Để phương trình có nghiệm cần : \(\(\(\(\Delta\ge0\)\)\)\)
hay \(\(\(\(\orbr{\begin{cases}a\ge2\\a\le-2\end{cases}}\)\)\)\)và \(\(\(\(\orbr{\begin{cases}b\ge2\sqrt{17}\\b\le-2\sqrt{17}\end{cases}\left(\cdot\right)}\)\)\)\)
Gọi \(\(\(\(t\)\)\)\)là nghiệm chung 2 phương trình , ta có :
\(\(\(\(\hept{\begin{cases}t^2+t.a+1=0\\t^2+t.b+17=0\end{cases}}\)\)\)\)
\(\(\(\(\Rightarrow t\left(a-b\right)-16=0\Rightarrow a-b=\frac{16}{t}\)\)\)\)
Giải phương trình \(\(\(\(\left(1\right)\)\)\)\): tìm \(\(\(\(t\)\)\)\)theo \(a\):
\(\(\(\(t=\frac{-a\pm\sqrt{a^2-4}}{2}\Rightarrow b=a-\frac{32}{-a\pm\sqrt{a^2-4}}\)\)\)\)
Kết hợp với \(\(\(\(\left(\cdot\right)\)\)\)\): \(\(\(\(b\in(-\infty;-2\sqrt{17}]\)\)\)\)∪\(\(\(\([2\sqrt{17};+\infty)\)\)\)\)
+) Với \(\(\(\(b=a-\frac{32}{\sqrt{a^2-4}-a}=\frac{544a+\sqrt{a^2-4}}{32}\)\)\)\)
Nếu \(\(\(\(a\ge2\)\)\)\)thì \(\(\(b\ge18\left(tm\right)\)\)\)
Nếu \(\(\(\(a\le-2\)\)\)\), Ta phải chứng minh \(\(\(\(32a+\sqrt{a^2-4}\le-4\sqrt{17}\)\)\)\)hay \(\(\(\(32a+4\sqrt{17}\le-\sqrt{a^2-4}\)\)\)\)
____________cạn, hình như sai ở đâu , để xem lại________
_Sorry_
_Minh ngụy_
___Giải PT (1), tìm t theo a :_
.....................
\(a\ge2\Rightarrow b\ge18\left(tm\right)\)
\(a\le2\Rightarrow......................\)(luôn đúng với mọi \(b\))
+) Nếu \(b=a-\frac{32}{-a-\sqrt{a^2-4}}=\frac{544a-\sqrt{a^2-4}}{32}\). cũng tương tự như trên , thỏa mãn với
\(a\in(-\infty;-2]\)U \([2;+\infty)\)
Như vậy , tìm được b theo a \(b=\frac{544a\pm\sqrt{a^2-4}}{32}\)
Suy ra \(|a|+|b|=a+\frac{544+\sqrt{a^2-4}}{32}\)
Giờ chỉ việc xét \(|a|\in[2;+\infty)\)là ra min và a,b nha
_Minh ngụy_

Gọi m là nghiệm chung của 2 phương trình thì ta có:
\(\hept{\begin{cases}m^2+am+6=0\\m^2+bm+12=0\end{cases}}\)
\(\Rightarrow2m^2+\left(a+b\right)m+18=0\)
Để phương trình có nghiệm thì
\(\Delta=\left(a+b\right)^2-144\ge0\)
\(\Leftrightarrow\left|a+b\right|\ge12\)
Ta lại có:
\(\left|a\right|+\left|b\right|\ge\left|a+b\right|\ge12\)
Tới đây thì đơn giản rồi nên b tự làm nhé.

Câu 2: Theo định lý Vi-et ta có \(\hept{\begin{cases}x_1+x_2=-a\\x_1x_2=b\end{cases}}\)Bất Đẳng Thức cần chứng minh có dạng
\(\frac{x_1}{1+x_1}+\frac{x_2}{1+x_2}\ge\frac{2\sqrt{x_1x_2}}{1+\sqrt{x_1x_2}}\)Hay \(\frac{x_1}{1+x_2}+1+\frac{x_2}{1+x_1}+1\ge\frac{2\sqrt{x_1x_2}}{1+\sqrt{x_1x_2}}+2\)
\(\left(x_1+x_2+1\right)\left(\frac{1}{1+x_1}+\frac{1}{1+x_2}\right)\ge\frac{2\left(1+2\sqrt{x_1x_2}\right)}{1+\sqrt{x_1x_2}}\)Theo Bất Đẳng Thức Cosi ta có
\(x_1+x_2+1\ge2\sqrt{x_1x_2}+1\)Để chứng minh (*) ta quy về chứng minh
\(\frac{1}{1+x_1}+\frac{1}{1+x_2}\ge\frac{2}{1+\sqrt{x_1x_2}}\)với \(x_1;x_2>1\). Quy đồng rồi rút gọn Bất Đẳng Thức trên tương đương với
\(\left(\sqrt{x_1x_2}-1\right)\left(\sqrt{x_1}-\sqrt{x_2}\right)^2\ge0\)(Điều này hiển nhiên đúng)
Dấu "=" xảy ra khi và chỉ khi \(x_1=x_2\Leftrightarrow a^2=4b\)

x = -2 là nghiệm của phương trình: a x 2 + bx + c = 0, ta có:
4a - 2b + c = 0
x = 3 là nghiệm của phương trình: a x 2 + bx + c = 0 ta có:
9a + 3b + c = 0
Ba số a, b, c là nghiệm của hệ phương trình