Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để đạt điểm tối đa, thí sinh phải trả lời rằng kích cỡ tối đa của cánh cửa là 1/6 của chu vi đường tròn, tính ra chính xác bằng đơn vị centi-mét.
pisa toán
Theo như biểu đồ ở phía trên, không khí sẽ di chuyển từ bên ngoài qua cửa vào tới thẳng cửa ra nếu như phần tường nằm giữa cửa ra và cửa vào ngắn hơn phần chu vi 2 cánh cửa liên tiếp chặn lại. Do mỗi phần tường có kích cỡ bằng đúng 1/3 chu vi căn phòng, và có 2 cánh cửa tương đương với 2/3 chu vi, do đó tổng kích cỡ cửa ra và cửa vào phải nhỏ hơn 1 – 2/3 = 1/3 chu vi. Do cửa ra và cửa vào có kích cỡ bằng nhau, mỗi cánh cửa sẽ phải nhỏ hơn (1/3)/2 = 1/6 chu vi của căn phòng.
Câu hỏi trên là một trong các câu hỏi khó nhất trong kì thi PISA, nằm ở phần trên của hạng khó nhất (Hạng 6). Câu hỏi này đòi hỏi thí sinh phải có tư duy tốt về hình học (không gian và hình dạng). Cũng bởi độ khó của câu hỏi này, thí sinh chỉ có thể đạt điểm tối đa, hoặc không đạt điểm nào. Dù chỉ đòi hỏi tư duy toán học căn bản, câu hỏi này đòi hỏi thí sinh phải phân tích một cách cẩn thận dựa trên tư duy hình học.
Để đạt điểm tối đa, thí sinh phải trả lời rằng kích cỡ tối đa của cánh cửa là 1/6 của chu vi đường tròn, tính ra chính xác bằng đơn vị centi-mét.
Theo như biểu đồ ở phía trên, không khí sẽ di chuyển từ bên ngoài qua cửa vào tới thẳng cửa ra nếu như phần tường nằm giữa cửa ra và cửa vào ngắn hơn phần chu vi 2 cánh cửa liên tiếp chặn lại. Do mỗi phần tường có kích cỡ bằng đúng 1/3 chu vi căn phòng, và có 2 cánh cửa tương đương với 2/3 chu vi, do đó tổng kích cỡ cửa ra và cửa vào phải nhỏ hơn 1 – 2/3 = 1/3 chu vi. Do cửa ra và cửa vào có kích cỡ bằng nhau, mỗi cánh cửa sẽ phải nhỏ hơn (1/3)/2 = 1/6 chu vi của căn phòng.
Câu hỏi trên là một trong các câu hỏi khó nhất trong kì thi PISA, nằm ở phần trên của hạng khó nhất (Hạng 6). Câu hỏi này đòi hỏi thí sinh phải có tư duy tốt về hình học (không gian và hình dạng). Cũng bởi độ khó của câu hỏi này, thí sinh chỉ có thể đạt điểm tối đa, hoặc không đạt điểm nào. Dù chỉ đòi hỏi tư duy toán học căn bản, câu hỏi này đòi hỏi thí sinh phải phân tích một cách cẩn thận dựa trên tư duy hình học.

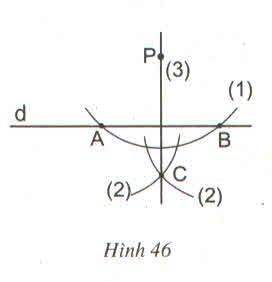
a) Ta có PA = PB (A, B nằm trên cung tròn có tâm P) CA = CB (hai cung tròn AB có tâm A và B có bán kính bằng nhau; C la giao điểm của 2 cung)
Vậy P; C cách đều A và B nên đường thẳng CP là đường trung trực của AB nên
PC ⊥ d
b) Một cách vẽ khác
- Lấy điểm A bất kì trên d
- Vẽ cung tròn tâm A bán kính AP cắt đường thẳng d tại M
- Vẽ cung tròn tâm M bán kính MP cắt cung tròn tâm A tại C
- Vẽ đường thẳng PC, đường thẳng PC chính là đường vuông góc với d.
=> PC ⊥ d (đpcm)
Hướng dẫn:
a) Ta có PA = PB (A, B nằm trên cung tròn có tâm P) CA = CB (hai cung tròn AB có tâm A và B có bán kính bằng nhau; C la giao điểm của 2 cung)
Vậy P; C cách đều A và B nên đường thẳng CP là đường trung trực của AB nên
PC ⊥ d
b) Một cách vẽ khác
- Lấy điểm A bất kì trên d
- Vẽ cung tròn tâm A bán kính AP cắt đường thẳng d tại M
- Vẽ cung tròn tâm M bán kính MP cắt cung tròn tâm A tại C
- Vẽ đường thẳng PC, đường thẳng PC chính là đường vuông góc với d.
=> PC ⊥ d (đpcm)

bạn tính diện tích hình vuông sau đó tính diện tích phần thừa và lấy hình vuông trừ phần thừa là ra đơn giản mà

Gọi AM, BN, CL là các trung tuyến của tam giác ABC
=> G là trọng tâm của tam giác ABC. Ta cần phải chứng minh S(GAB)=S(GBC)=S(GAC).
+ Hai tam giác AMC và tam giác ABC có chung đường cao hạ từ A xuống BC nên
S(AMC)/S(ABC)=MC/BC=1/2 => S(AMC)=S(ABC)/2 (1)
+ Hai tam giác GAC và tam giác AMC có chung đường cao hạ từ C xuống AM nên
S(GAC)/S(AMC)=AG/AM=2/3 (3 đường trung tuyến cắt nhau tại 1/3 mmỗi đường kể từ đáy)
=> S(GAC)=2.S(AMC)/3 (2)
Từ (1) và (2) => S(GAC)=S(ABC)/3
+ Tương tự cũng c/m được
S(GAB)=S(GBC)=S(ABC)/3
=> Trọng tâm của tam giác khi nối với đỉnh của tam giác ABC thì chia tam giác ABC thành 3 tam giác nhỏ có diện tích bằng nhau
Bạn đặt tên cho các đỉnh rồi chứng minh các tam giác đó bằng nhau nha

Câu trả lời đúng trong các câu sau là :
A. Hai đường thẳng cắt nhau thì vuông góc
B. Hai đường thẳng vuông góc thì cắt nhau
C. Hai đường thẳng vuông góc chỉ tạo thành một góc vuông
D. Hai đường thẳng vuông góc tạo thành hai góc vuông