Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Các đường trung tuyến cắt nhau tại trọng tâm
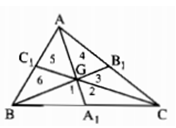
=> vẽ hình ra sẽ nhận thấy 6 tam giác: Tam giác ABC trọng tâm G
Xét 2 tam giác có đáy chung cạnh thì hiển nhiên diện tích bằng nhau do có chung đương cao và đáy bằng nhau => diện tích bằng 1/2 diện tích tam giác đỉnh G đáy là canh tam giác ABC
Xét các tam giác đỉnh G đáy là cạnh của tam giác ABC có 3 tam giác đó có diện tích bằng nhau
Từ 2 điều trên => diện tích 6 tam giác nhỏ đó = nhau

Hình vẽ:
Xét sáu tam giác được đánh số là: 1, 2, 3, 4, 5, 6
Vì G là trọng tâm nên ta có:
\(S_{GAB}=S_{GBC}=S_{GCA}=\dfrac{1}{3}S_{ABC}\)
Ta lại có \(S_1=S_2;S_3=S_4;S_5=S_6\) (vì mỗi cặp tam giác có chung đường cao và hai đáy bằng nhau, vậy sáu tam giác 1, 2, 3, 4, 5, 6 có diện tích bằng nhau)

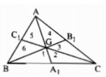
Xét sáu tam giác được đánh số là: 1, 2, 3, 4, 5, 6
Chứng minh hoàn toàn tương tự như bài 4.4 ta có
SGAB = SGBC = SGCA = 1/3 SABC
Ta lại có S1 = S2, S3 = S4, S5 = S6 (vì mỗi cặp tam giác có chung đường cao và hai đáy bằng nhau, vậy sáu tam giác 1, 2, 3, 4, 5, 6 có diện tích bằng nhau)

Xét ΔABM có AHvừa là đường cao, vừa là phân giác
nên ΔABM cân tại A
=>H là trung điểm của BM
Xét ΔAHC có AM là phân giác
nên AH/AC=CM/MH=CM/2MB=CM/2MC=1/2
Xet ΔAHC vuông tại H có sin ACH=AH/AC=1/2
nên góc ACH=30 độ
=>góc HAC=60 độ
=>góc BAH=1/2*góc HAC=30 độ
=>góc BAC=90 độ
=>ΔABC vuông tại A
Xét ΔABC vuông tại A có góc B+góc C=90 độ
=>góc B=60 độ
mà ΔAMB cân tại A
nên ΔAMB đều
Xét ΔABM có AHvừa là đường cao, vừa là phân giác
nên ΔABM cân tại A
=>H là trung điểm của BM
Xét ΔAHC có AM là phân giác
nên AH/AC=CM/MH=CM/2MB=CM/2MC=1/2
Xet ΔAHC vuông tại H có sin ACH=AH/AC=1/2
nên góc ACH=30 độ
=>góc HAC=60 độ
=>góc BAH=1/2*góc HAC=30 độ
=>góc BAC=90 độ
=>ΔABC vuông tại A
Xét ΔABC vuông tại A có góc B+góc C=90 độ
=>góc B=60 độ
mà ΔAMB cân tại A
nên ΔAMB đều

Xét ΔABM có AHvừa là đường cao, vừa là phân giác
nên ΔABM cân tại A
=>H là trung điểm của BM
Xét ΔAHC có AM là phân giác
nên AH/AC=CM/MH=CM/2MB=CM/2MC=1/2
Xet ΔAHC vuông tại H có sin ACH=AH/AC=1/2
nên góc ACH=30 độ
=>góc HAC=60 độ
=>góc BAH=1/2*góc HAC=30 độ
=>góc BAC=90 độ
=>ΔABC vuông tại A
Xét ΔABC vuông tại A có góc B+góc C=90 độ
=>góc B=60 độ
mà ΔAMB cân tại A
nên ΔAMB đều
Xét ΔABM có AHvừa là đường cao, vừa là phân giác
nên ΔABM cân tại A
=>H là trung điểm của BM
Xét ΔAHC có AM là phân giác
nên AH/AC=CM/MH=CM/2MB=CM/2MC=1/2
Xet ΔAHC vuông tại H có sin ACH=AH/AC=1/2
nên góc ACH=30 độ
=>góc HAC=60 độ
=>góc BAH=1/2*góc HAC=30 độ
=>góc BAC=90 độ
=>ΔABC vuông tại A
Xét ΔABC vuông tại A có góc B+góc C=90 độ
=>góc B=60 độ
mà ΔAMB cân tại A
nên ΔAMB đều
Gọi AM, BN, CL là các trung tuyến của tam giác ABC
=> G là trọng tâm của tam giác ABC. Ta cần phải chứng minh S(GAB)=S(GBC)=S(GAC).
+ Hai tam giác AMC và tam giác ABC có chung đường cao hạ từ A xuống BC nên
S(AMC)/S(ABC)=MC/BC=1/2 => S(AMC)=S(ABC)/2 (1)
+ Hai tam giác GAC và tam giác AMC có chung đường cao hạ từ C xuống AM nên
S(GAC)/S(AMC)=AG/AM=2/3 (3 đường trung tuyến cắt nhau tại 1/3 mmỗi đường kể từ đáy)
=> S(GAC)=2.S(AMC)/3 (2)
Từ (1) và (2) => S(GAC)=S(ABC)/3
+ Tương tự cũng c/m được
S(GAB)=S(GBC)=S(ABC)/3
=> Trọng tâm của tam giác khi nối với đỉnh của tam giác ABC thì chia tam giác ABC thành 3 tam giác nhỏ có diện tích bằng nhau
Bạn đặt tên cho các đỉnh rồi chứng minh các tam giác đó bằng nhau nha