
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



ta có : a.b = 24 (1)
a + b = -10 (2)
Từ (2) => a = -10 - b thay vào (1)
=> b( - 10 - b ) = 24
<=> b2+ 10b + 24 = 0
<=> b = -4 => a = -6 hoặc b = -6 => a = -4
ta có : a.b = 24 (1)
a + b = -10 (2)
Từ (2) => a = -10 - b thay vào (1)
=> b( - 10 - b ) = 24
<=> b2+ 10b + 24 = 0
<=> b = -4 => a = -6 hoặc b = -6 => a = -4


Đáp án A.
Cách 1:
∫ 1 2 2 d x x 3 + 3 x 2 + 2 x = 2. ∫ 1 2 1 x x + 1 x + 2 d x = 2 3 . ∫ 1 2 1 x x + 2 + 1 x x + 1 − 2 x + 1 x + 2 d x
= 2 3 ∫ 1 2 1 2 x − 1 2 x + 4 + 1 x − 1 x + 1 − 2 x + 1 + 2 x + 2 d x
∲ = 2 3 ∫ 1 2 3 2 . 1 x − 3 x + 1 + 3 2 . 1 x + 2 d x = ∫ 1 2 1 x d x − 2. ∫ 1 2 1 x + 1 d x + ∫ 1 2 1 x + 2 d x
= ln x 1 2 − 2. ln x + 1 1 2 + ln x + 2 1 2 = ln 2 − ln 1 − 2. ln 3 − ln 2 + ln 4 − ln 3 = ln 32 27
⇒ a = 32 ; b = 27 ⇒ a + b = 59
Cách 2: Sử dụng máy tính.

Lúc này ∫ 1 2 2 d x x 3 + 3 x 2 + 2 x = A n s .
Suy ra a b = e A n s
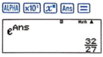
⇒ a b = 32 27 ⇒ a + b = 59

4a.
Số tự nhiên là A, ta có:
A = 7m + 5
A = 13n + 4
=>
A + 9 = 7m + 14 = 7(m + 2)
A + 9 = 13n + 13 = 13(n+1)
vậy A + 9 là bội số chung của 7 và 13
=> A + 9 = k.7.13 = 91k
<=> A = 91k - 9 = 91(k-1) + 82
vậy A chia cho 91 dư 82
4b.
Giả sử p là 1 số nguyên tố >3, do p không chia hết cho 3 nên p có dạng 3k + 1 hoặc 3k + 2
Vì p +4 là số nguyên tố nên p không thể có dạng 3k + 2
Vậy p có dạng 3k +1.
=> p + 8 = 3k + 9 chia hết cho 3 nên nó là hợp số.

Ta có:
\(66a+55b=11.6a+11.5b=11.\left(6a+5b\right)\) \(\text{⋮}\) \(11\)
Mà \(111011\)⋮̸\(11\)
Vì vậy không thể tìm được 2 số tự nhiên a và b để \(66a+55b=111011\)

\(\frac{16^2-b^2+7}{a^3+78-43.2}=107\)
\(\Rightarrow16^2-b^2+7=107a^3+78.107-43.2.107\)
\(\Rightarrow256-b^2+7=107a^3+8346-9202\)
\(\Rightarrow263-b^2=107a^3-856\)
\(\Rightarrow263-b^2+856=107a^3\)
\(\Rightarrow1119=107a^3+b^2\)
Ta có:
\(107a^3<1119\)
\(\Rightarrow a^3\le10\)
Mà a là số tự nhiên nên \(a^3\in\left\{0;1;8\right\}\)
\(\Rightarrow a\in\left\{0;1;2\right\}\)
Với a=0
\(b^2=1119\)
Mà 1119 không phải số chính phương
-> Loại
Với a=1
\(b^2=1119-107.1^3=1012\)
Mà 1012 không là số chính phương
-> Loại
Với a=2
\(b^2=1119-107.8=263\)
263 không phải số chính phương
-> Loại
Vậy không có a, b thỏa mãn.

vì a/b=15/35=3/7
=>a:3=b:7
=>a=3/7b
mà ƯCLN(a,b).BCNN(a,b)=a.b
=>3/7b.b=3549
=>b=91, a=3/7b=39
Ta có: \(\frac{a}{b}\)= \(\frac{15}{35}\)= \(\frac{3}{7}\).
Suy ra: a= 3K; b= 7K, với k thuộc N*.
Ta có: ƯCLN (a,b)= ƯCLN(3K,7K)= K

1+2+3+...+n=[n.(n+1)]:2
Ta có 1+2+3+...+n=aaa
=>[n.(n+1)]:2=aaa=a.111=a.3.37
=>n.(n+1)=a.3.37.2=(a.3.2).37=6a.37
Nhận thấy n.(n+1) là tích 2 số tự nhiên liên tiếp
=>6a.37 cũng là tích 2 số tự nhiên liên tiếp
Xét:
+)6a=36=>a=6( thỏa mãn)
+)6a=38=>a=19/3( ko thỏa mãn a là số tự nhiên)
Do đó a=6
Thay a=6 vào 6a.37=6.6.37=36.37=1332
Khi đó n.(n+1)=1332=36.37=36.(36+1)
=>n=36
Vậy a=6;n=36
Từ 1 đến n có n số hạng
=> 1 + 2 + .... + n = \(\frac{\left(n+1\right)n}{2}\)
Mà theo bài ra ta có : 1 + 2 + 3 + ... + n = aaa
=> \(\frac{\left(n+1\right)n}{2}\) = aaa
=> n.( n + 1 ) = 2.3.37.a
Vì tích n.( n + 1 ) chia hết cho nguyên tố 37 nên n hoặc n + 1 chia hết cho 37
Vì \(\frac{n\left(n+1\right)}{2}\) có 3 chữ số => n + 1 < 74 => n = 37 hoặc n + 1 = 37
+) với n = 37 thì \(\frac{37.38}{2}\) = 703 ( loại )
+) với n + 1 = 37 thì \(\frac{36.37}{2}\) = 666 ( thỏa mãn )
Vậy n = 36 và a = 6 . Ta có 1 + 2 + 3 + .... + 36 = 666
a và b la 12 va 18
ƯCLN(a,b)=32. Đặt a= 6x ; b= 6y
với ƯCLN(x,y)=1 và x,y ∈ N
ta có : a.b=216
6x.6y=216
x.y=216:(6.6)
x.y= 6
từ trên ta có bảng:
do đó, ta có:
a=6.1=6;b=6.6=36
a=6.2=12;b=6.3=18
a=6.3=18;b=6.2=12
a=6.6=36;b=6.1=6
CHÚC BẠN LÀM TỐT NHÉ!