Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(i = \frac{\lambda D}{a}=\frac{0,5.2}{0,5}= 2mm.\)
Số vân sáng trên màn quan sát là
\(N_s= 2.[\frac{L}{2i}]+1 =2.6+1 = 13.\)
Chọn C
vân sáng bậc 3 cách vân trung tâm 2,4 mm tức là: x0+3 - x0 = 2,4 mm <=> 3i = 2,4 => i = 0,8mm
Bước sóng của ánh sáng đơn sắc dùng trong thí nghiệm là:
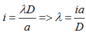
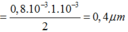
- Khoảng vân giao thoa
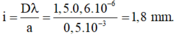
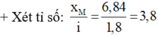
→ M gần vân sáng bậc 3 về phía vân sáng trung tâm.
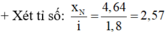
→ N gần vân sáng bậc 2 về phía vân sáng trung tâm.
⇒ Trên MN có 6 vân sáng ứng với:
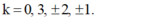
Đáp án A
+ Khoảng vân giao thoa
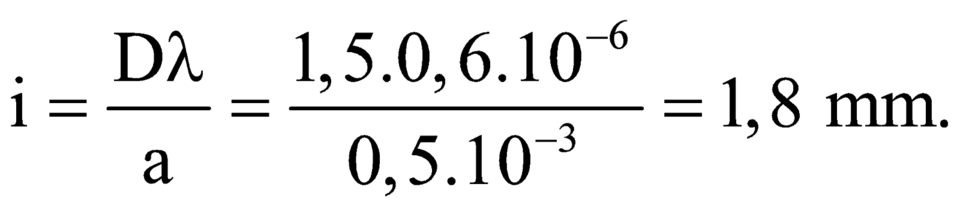
Xét tỉ số 
M gần vân sáng bậc 3 về phía vân sáng trung tâm.
Xét tỉ số 
N gần vân sáng bậc 2 về phía vân sáng trung tâm.
Trên MN có 6 vân sáng ứng với 
Đáp án C
Vân sáng bậc 3 cách vân trung tâm 2,4mm => Khoảng vân
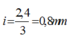
Nên áp dụng công thức tính khoảng vân ta có:
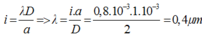
Phương pháp: Sử dụng công thức tính khoảng vân và công thức xác định vị trí vân sáng, tối
Cách giải:
Vân sáng bậc 3 cách vân trung tâm 2,4mm => Khoảng vân i = 2,4/3 = 0,8 mm
Nên áp dụng công thức tính khoảng vân ta có:
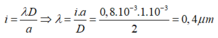
Đáp án C
Khoảng cách lớn nhất từ giả thiết nghĩa là khoảng cách từ vân sáng bậc 2 (nửa trên) đến vân tối thứ 4 (nửa dưới)
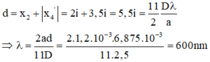
Đáp án D
Vân sáng bậc 4 cách vân trung tâm là
\(x_ 4 = 4.i = 4.\frac{\lambda D}{a} = 3,2mm.\)
Chú ý nếu giữ nguyênđơn vị của \(\lambda (\mu m)\), D(m), a(mm) thì khi đó kết quả cho \(x\) ra đơn vị là mm.
A( mặc dù ko bít có đúng ko nhưng mong tích cho mình nhé