

![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


![]()

- Khoảng vân giao thoa
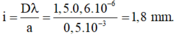
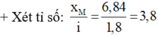
→ M gần vân sáng bậc 3 về phía vân sáng trung tâm.
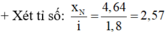
→ N gần vân sáng bậc 2 về phía vân sáng trung tâm.
⇒ Trên MN có 6 vân sáng ứng với:
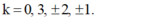

Đáp án A
+ Khoảng vân giao thoa
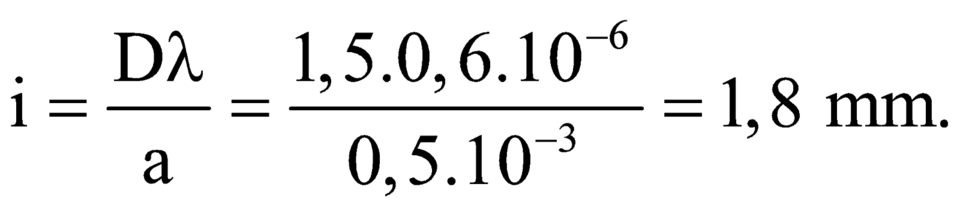
Xét tỉ số ![]() M gần vân sáng bậc 3 về phía vân sáng trung tâm.
M gần vân sáng bậc 3 về phía vân sáng trung tâm.
Xét tỉ số ![]() N gần vân sáng bậc 2 về phía vân sáng trung tâm.
N gần vân sáng bậc 2 về phía vân sáng trung tâm.
![]() Trên MN có 6 vân sáng ứng với
Trên MN có 6 vân sáng ứng với ![]()

Đổi đơn vị: \(\lambda_1=450n m= 0,45 \mu m.\)
\(\lambda_1=600n m= 0,6 \mu m.\)
Hai vân sáng trùng nhau khi \(k_1i_1=k_2i_2 \)
<=> \(\frac{k_1}{k_2}= \frac{i_1}{i_2}=>\frac{k_1}{k_2}= \frac{\lambda_1}{\lambda_2} =\frac{3}{4}\ \ (*)\)
Xét trong đoạn MN nên \(5,5 mm \leq x_s \leq 22mm. \)
<=> \(5,5 mm \leq k_1\frac{\lambda_1 D}{a} \leq 22mm. \)
<=> \(\frac{5,5.a}{\lambda_1 D} \leq k_1\leq \frac{22.a}{\lambda_1 D}\)
Giữ nguyên đơn vị của a = 0,5 mm; D = 2m; \(\lambda_1=0,45 \mu m.\)
<=> \(3,055 \leq k_1 \leq 12,22\)
Kết hợp với (*) ta có \(k_1\) chỉ có thể nhận giá trị : 3x2= 6; 3x3 = 9; 3x4 =12.
Như vậy có 3 vị trí trùng nhau của hai bức xạ trong đoạn MN.

Đáp án D
Lời giải chi tiết:
Tổng quát cách tìm số vân sáng trên vùng giao thoa MN là số giá trị của k thỏa mãn:


Vậy có 6 giá trị của k nguyên tương ứng với 6 vân sáng.

\(i = \frac{\lambda D}{a}=\frac{0,5.2}{0,5}= 2mm.\)
Số vân sáng trên màn quan sát là
\(N_s= 2.[\frac{L}{2i}]+1 =2.6+1 = 13.\)

Chọn đáp án B
@ Lời giải:
+ Khoảng vân: i = λ D a = 2 m m ⇒ Vị trí vân sáng x = k i = 2 k .
+ Vì M và N ở khác phía vân trung tâm nên x M và x N trái dấu. Chọn:
x M = − 5 , 9 c m ⇒ x N = 9 , 7 c m .
+ Số vân sáng có trong khoảng giữa MN: x M < x < x N ⇔ − 5 , 9 < 2 k < 9 , 7 ⇒ − 2 , 95 < k < 4 , 85 .
⇒ k = − 2 ; − 1 ; 0 ; 1 ; 2 ; 3 ; 4 ⇒ Có 7 giá trị của k
+ Khối lượng urani 92 235 U cần dùng: m = N . A N A = 2 , 46375.10 27 .235 6 , 02.10 23 = 961762 , 87 g ≈ 962 k g .