
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tập xác định của phương trình
- 2
Rút gọn thừa số chung
- 3
Đơn giản biểu thức
- 4
Biệt thức
- 5
Biệt thức
- 6
Nghiệm
- 7
Lời giải thu được

Đặt \(t=\left|x-1\right|,t\ge0\)
Suy ra pt trở thành : \(t^2+t-2016=0\)
Xét \(\Delta=1^2-4.\left(-2016\right)=8065\)
\(\Rightarrow\begin{cases}t_1=\frac{-1-\sqrt{8065}}{2}\left(\text{loại}\right)\\t_2=\frac{-1+\sqrt{8065}}{2}\left(\text{nhận}\right)\end{cases}\)
Ta có \(\left|x-1\right|=\frac{-1+\sqrt{8065}}{2}\)
+ Nếu \(x\ge1\) thì \(x-1=\frac{-1+\sqrt{8065}}{2}\Rightarrow x=\frac{1+\sqrt{8065}}{2}\)(tm)
+ Nếu x < 1 thì \(1-x=\frac{-1+\sqrt{8065}}{2}\Rightarrow x=\frac{3-\sqrt{8065}}{2}\) (tm)

Điều kiện \(x\ge0\)
\(\sqrt{x}=x\Leftrightarrow\sqrt{x}\left(1-\sqrt{x}\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=0\\x=1\end{cases}}\)

Ta có (x + |x| + 2016)(y + |y| + 2016) > 2016 với mọi x, y nên không thể tính được P

Điều kiện: x - 2 ≥ 0 ⇔ x ≥ 2
Ta có: x - 2 ≥ 3 ⇔ x - 2 ≥ 3 ⇔ x ≥ 5
Giá trị x ≥ 5 thỏa mãn điều kiện.
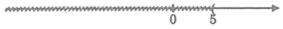

Ta có : x2 + x - p = 0 <=> x(x + 1) = p
Ta có : x và x + 1 là 2 số nguyên liên tiếp => x(x + 1) chia hết cho 2 => p chia hết cho 2 => p = 2
=> x(x + 1) = 2 <=> x2 + x - 2 = 0 => x1 = 1; x2 = -2
Tập hợp cần tìm là {-2; 1}

\(\Leftrightarrow0\le\sqrt{3-2x}\le\sqrt{5}\\ \Leftrightarrow0\le3-2x\le5\\ \Leftrightarrow-1\le x\le\dfrac{3}{2}\)