Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có\(\Delta ABC=\Delta DEF\)(1)
=> \(\hept{\begin{cases}AB=DE\\AC=DF\\BC=EF\end{cases}}\)(cạnh tương ứng) => EF = 8 cm
Tư (1) => \(\widehat{A}=\widehat{D}\)(góc tương ứng)
Lại có trong \(\Delta ABC\)có \(\widehat{A}+\widehat{B}+\widehat{C}=180^{\text{o}}\)
=> \(\widehat{A}+70^{\text{o}}+40^{\text{o}}=180^{\text{o}}\)
=> \(\widehat{A}=70^{\text{o}}\)
=> \(\widehat{D}=70^{\text{o}}\)

A B C D E F
Xét t/giác DEF có \(\widehat{D}+\widehat{E}+\widehat{F}=180^0\) (tổng 3 góc của 1 t/giác)
=> \(\widehat{D}=180^0-\widehat{E}-\widehat{F}=180^0-70^0-60^0=50^0\)
Xét t/giác ABC và t/giác DEF
có: AB = DE (gt)
AC = DF (gt)
\(\widehat{A}=\widehat{D}=50^0\)
=> t/giác ABC = t/giác DEF (c.g.c)

Bài 3:
a: Xét ΔABD và ΔACD có
AB=AC
AD chung
BD=CD
Do đó: ΔABD=ΔACD
b: Ta có: ΔABD=ΔACD
nên \(\widehat{BAD}=\widehat{CAD}\)
c: Ta có: ΔABC cân tại A
mà AD là đường trung tuyến
nên AD là đường cao

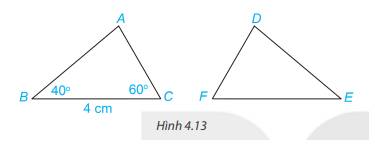
Vì \(\Delta ABC = \Delta DEF\) nên BC = EF ( 2 cạnh tương ứng); \(\widehat A = \widehat {EDF}\) ( 2 góc tương ứng)
Mà BC = 4 cm nên EF = 4 cm
Trong tam giác ABC có: \(\widehat A + \widehat B + \widehat C = 180^\circ \) ( định lí tổng ba góc trong một tam giác)
\(\begin{array}{l} \Rightarrow \widehat A + 40^\circ + 60^\circ = 180^\circ \\ \Rightarrow \widehat A = 180^\circ - 40^\circ - 60^\circ = 80^\circ \end{array}\)
Mà \(\widehat A = \widehat {EDF}\) nên \(\widehat {EDF} = 80^\circ \)
Giải:
Ta có tam giác ABC= tam giác DEF
=>Góc D+Góc E+Góc F=Góc A+Góc B+Góc C=180độ (Tổng 3 góc của tam giác)
mà Góc B=Góc E(2 góc tương ứng)
Góc C=Góc F(2 góc tương ứng)
=>Góc D+Góc B+Góc C= 180độ
T/S: Góc D= 180-70-40(độ)
=70độ
=>Góc D=70độ
Ta thấy BC=EF(2 cạnh tương ứng)
=>BC=EF(=8)
=>EF=8cm
( * ) Vì \(\Delta\)ABC = \(\Delta\)DEF nên EF = BC = 8 cm
( * ) \(\Delta\)ABC có :
 + góc B + góc C = 180 ( tổng 3 góc tam giác )
\(\Rightarrow\)Â + 70 + 40 = 180
\(\Rightarrow\)Â = 180 - ( 70 + 40 ) = 70
Vì \(\Delta\)ABC = \(\Delta\)DEF nên góc D = Â = 70