Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABE vuông tại E và ΔACF vuông tại F có
góc BAE chung
DO đó: ΔABE\(\sim\)ΔACF
SUy ra: AB/AC=AE/AF
hay \(AB\cdot AF=AE\cdot AC\)
b: Xét ΔAEF và ΔABC có
AE/AB=AF/AC
góc EAF chung
Do đó: ΔAEF\(\sim\)ΔABC
Suy ra: \(\widehat{AEF}=\widehat{ABC}\)

a: góc AEH+góc AFH=180 độ
=>AEHF nội tiếp
b; góc ABD=1/2*180=90 độ
=>BD vuông góc AB
=>BD//CH
góc ACD=1/2*180=90 độ
=>CD vuông góc AC
=>CD//BH
Xét tứ giác BHCD có
BH//CD
BD//CH
=>BHCD là hbh
=>BC cắt HDtại trung điểm của mỗi đường
=>H,M,D thẳng hàng

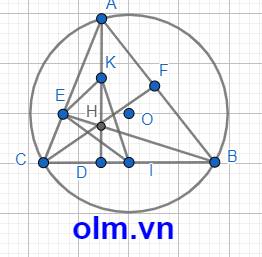
a, Xét tam giác vuông EBC vuông tại E và CI = IB
⇒ IE = IC = IB (1) ( vì trong tam giác vuông trung tuyến ứng với cạnh huyền bằng \(\dfrac{1}{2}\) cạnh huyền)
Xét tam giác vuông BCF vuông tại F và IC =IB
⇒IF = IC = IB (2) (vì trong tam giác vuông trung tuyến ứng với cạnh huyền bằng \(\dfrac{1}{2}\) cạnh huyền)
Từ (1) và (2) ta có:
IE = IF = IB = IC
Vậy bốn điểm B, C, E, F cùng thuộc một đường tròn tâm I bán kính bằng \(\dfrac{1}{2}\) BC (đpcm)
b, Xét \(\Delta\)AFC và \(\Delta\)AEB có:
\(\widehat{CAF}\) chung ; \(\widehat{AFC}\) = \(\widehat{AEB}\) = 900
⇒ \(\Delta\)AFC \(\sim\) \(\Delta\)AEB (g-g)
⇒ \(\dfrac{AF}{AE}\) = \(\dfrac{AC}{AB}\) (theo định nghĩa hai tam giác đồng dạng)
⇒AB.AF = AC.AE (đpcm)
Xét tam giác vuông AEH vuông tại E và KA = KH
⇒ KE = KH ( vì trong tam giác vuông trung tuyến ứng với cạnh huyền bằng \(\dfrac{1}{2}\) cạnh huyền)
⇒\(\Delta\)EKH cân tại K ⇒ \(\widehat{KEH}\) = \(\widehat{EHK}\)
\(\widehat{EHK}\) = \(\widehat{DHB}\) (vì hai góc đối đỉnh)
⇒ \(\widehat{KEH}\) = \(\widehat{DHB}\) ( tc bắc cầu) (3)
Theo (1) ta có: IE = IB ⇒ \(\Delta\) IEB cân tại I
⇒ \(\widehat{IEB}\) = \(\widehat{IBE}\) (4)
Cộng vế với vế của (3) và(4)
Ta có: \(\widehat{KEI}\) = \(\widehat{KEH}\) + \(\widehat{IEB}\) = \(\widehat{DHB}\) + \(\widehat{IBE}\) = \(\widehat{DHB}\) + \(\widehat{DBH}\)
Vì tam giác DHB vuông tại D nên \(\widehat{DHB}\) + \(\widehat{DBH}\) = 1800 - 900 = 900
⇒\(\widehat{KEI}\) = 900
IE \(\perp\) KE (đpcm)

a) Xét tứ giác BFEC có
\(\widehat{BFC}=\widehat{BEC}\left(=90^0\right)\)
nên BFEC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
\(\widehat{BAE}\) chung
Do đó: ΔAEB\(\sim\)ΔAFC(g-g)
Suy ra: \(\dfrac{AE}{AF}=\dfrac{AB}{AC}\)
hay \(AE\cdot AC=AB\cdot AF\)

Xét tứ giác BFEC có
\(\widehat{BFC}=\widehat{BEC}=90^0\)
=>BFEC là tứ giác nội tiếp đường tròn đường kính BC
Xét tứ giác AFHE có
\(\widehat{AFH}+\widehat{AEH}=90^0+90^0=180^0\)
=>AEHF là tứ giác nội tiếp
=>\(\widehat{HFE}=\widehat{HAC}=90^0-\widehat{ACB}\)
Xét tứ giác BFHD có
\(\widehat{BFH}+\widehat{BDH}=180^0\)
=>BFHD là tứ giác nội tiếp
=>\(\widehat{HFD}=\widehat{HBD}=90^0-\widehat{C}\)
\(\widehat{EFD}=\widehat{EFC}+\widehat{DFC}=90^0-\widehat{C}+90^0-\widehat{C}=180^0-2\cdot\widehat{C}\)
ΔEBC vuông tại E có EM là trung tuyến
nên ME=MB=MC
ME=MB và ME=MC
=>ΔMEB cân tại M và ΔMEC cân tại M
Xét ΔMEC có \(\widehat{EMB}\) là góc ngoài tại đỉnh M
nên \(\widehat{EMB}=\widehat{MEC}+\widehat{MCE}=2\cdot\widehat{C}\)
=>\(\widehat{EMD}+\widehat{EFD}=180^0-2\cdot\widehat{C}+2\cdot\widehat{C}=180^0\)
=>EFDM là tứ giác nội tiếp